Algèbre des parties d'un ensemble
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SGQC
- Messages: 4
- Enregistré le: 15 Fév 2018, 03:55
-
 par SGQC » 15 Fév 2018, 04:02
par SGQC » 15 Fév 2018, 04:02
Bonjour! J'ai de la misère avec une question que mon professeur m'a fait part. J'aimerais avoir de l'aide avec ce problème puisque je me suis casser la tète pendant 3 heures d'affiler sans avoir trouver de réponse.
Voici la question: Montrez que (A\B) Δ (B\C) = (A\B) ∪ (B\C)
A, B, C sont des ensembles dont le contenu est inconnu.
Merci de m'aider si possible!


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Fév 2018, 08:04
par chan79 » 15 Fév 2018, 08:04
SGQC a écrit:
Voici la question: Montrez que (A\B) Δ (B\C) = (A\B) ∪ (B\C)
Bonjour
Compte tenu de la définition de

, tu as juste à montrer que A\B et B\C sont disjoints.
-
SGQC
- Messages: 4
- Enregistré le: 15 Fév 2018, 03:55
-
 par SGQC » 15 Fév 2018, 13:51
par SGQC » 15 Fév 2018, 13:51
Je ne suis pas sur de suivre, pourrais tu expliquer s'il te plait?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Fév 2018, 14:24
par Ben314 » 15 Fév 2018, 14:24
Salut,
SGQC a écrit:Je ne suis pas sur de suivre, pourrais tu expliquer s'il te plait?
Pour deux parties F et G d'un même ensemble E,
- C'est quoi
la définition de la partie

?
- Vu cette définition, dans quel cas est-on sûr d'avoir
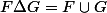
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
SGQC
- Messages: 4
- Enregistré le: 15 Fév 2018, 03:55
-
 par SGQC » 15 Fév 2018, 14:53
par SGQC » 15 Fév 2018, 14:53
Ben314 a écrit:Salut,
SGQC a écrit:Je ne suis pas sur de suivre, pourrais tu expliquer s'il te plait?
Pour deux parties F et G d'un même ensemble E,
- C'est quoi
la définition de la partie

?
- Vu cette définition, dans quel cas est-on sûr d'avoir
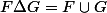
?
Du coup, la définition que j'ai est: << Soient A et B deux ensembles. La différence symétrique, notée A △ B, est l'union des ensembles A \ B et B \ A. Autrement dit: A△B = (A\B) ∪ (B\A) >>
Donc F△G = (F\G)∪(G\F) = (F∩G')∪(G∩F')
Comment est ce que (F∩G')∪(G∩F') = (F∪G)?
Est ce que je me suis planté quelque part solide? Car je n'y comprend rien.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Fév 2018, 15:12
par Ben314 » 15 Fév 2018, 15:12
Avec cette définition là de

, c'est effectivement un peu moins évident.
Donc commence par montrer qu'en fait les éléments de

, c'est ceux qui sont dans F ou dans G, mais pas dans les deux à la fois (c'est ce qu'on appelle le "ou exclusif") et donc que
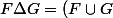\backslash (F\cap G))
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Fév 2018, 15:15
par Ben314 » 15 Fév 2018, 15:15
Sinon, pour répondre précisément à cette question là :
SGQC a écrit:Comment est ce que (F∩G')∪(G∩F') = (F∪G) ?
Pour que (F∩G')∪(G∩F') ce soit la même chose que (F∪G), il suffit (*) évidement que l'on ait F∩G'=F et G∩F'=G c'est àa dire que ...
(*) En fait c'est un "
il faut et il suffit", mais le "il faut" est moins clair que le "il suffit" qui lui est complètement évident.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
SGQC
- Messages: 4
- Enregistré le: 15 Fév 2018, 03:55
-
 par SGQC » 15 Fév 2018, 16:18
par SGQC » 15 Fév 2018, 16:18
Donc, si on revient a mon exercice et que j'ai bien compris:
(A\B) Δ (B\C) = (A\B) ∪ (B\C)
(A∪B) \ (B∩C) = (A\B) ∪ (B\C) | Autre façon de l’écrire
(A∪B) ∩ (B∩C)' = (A∩B') ∪ (B∩C') | Autre façon d’écrire les différence
(A∪B) ∩ (B'∪C') = (A∩B') ∪ (B∩C') | Loi de Morgan
Pour que (A∪B) ∩ (B'∪C') soit égal a (A∩B') ∪ (B∩C'), il suffit que l'on ait A∩B' = A et B∩C' = B
(A∪B) ∩ (B'∪C') = (A ∪ B)
(B'∪C') = Univers
(A∪B) ∩ Univers | Élément neutre
(A∪B) = (A∪B)
Sa marche mais est ce que je l'ai bien fait?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Fév 2018, 17:17
par Ben314 » 15 Fév 2018, 17:17
SGQC a écrit:(A\B) Δ (B\C) = (A\B) ∪ (B\C)
(A∪B) \ (B∩C) = (A\B) ∪ (B\C) | Autre façon de l’écrire
Ben... non... :
E F
F=(
E∪
F)\(
E∩
F)
donc
(A\B) (B\C)
(B\C)=
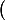 (A\B)
(A\B)∪
(B\C))
\
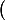 (A\B)
(A\B)∩
(B\C))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
?
?