Exercice " intégration par parties " TS

[nathalia33]

Bonjour , mon professeur de math m'a donnée cet exercice a faire pendant les vacances , et ca fait deux jours que je passe a bloquer complètement dessus , du coup je m'adresse a vous , en espérant que vous sauriez m'aider !
alors , voici l'énoncé :

u et v sont deux fonctions dérivables sur un intervalle I dont les dérivées u' et v' sont continues sur I.

1. Montrer que , pour tous nombres réels a et b de I ,
integr(b...a) u'(x)v(x)dx=[u(x)v(x)](b...a) - integr(b...a) u(x)v'(x)dx


--> Pour cette question je pense m'en être sortie , je l'ai fait a partir de (uv)'=u'v+uv'

2. On définit la suite (Kn) pour tout nombre entier naturel n non nul par
Kn=integr(1...0) (x^n)(e^-x)dx.

a) Calculer K1 à l'aide de la question 1.

pour cette question je bloque totalement , disons que j'arrive meme plus a calculer F(x) pour K1, je ne sais pas quelle formule utiliser .. ce qui m'empêche de répondre à la question si je comprend ?

ce qui fait que pour la suite , ca reste une totale catastrophe ..

b) démontrer que , pour tout n > ou égal a 1,
Kn+1 = -(1/e)+(n+1)Kn

c) calculer Ké et K".

d) en déduire la valeur de l'intégrale :
intergr(1...0) ((x^3)-(x^2)-x+1)e^-xdx


Je demande bien sure pas de réponse , mais des explications , de quoi me mettre sur la voie si possible ... Merci beaucoup !

[Kikoo <3 Bieber]

Bonjour , mon professeur de math m'a donnée cet exercice a faire pendant les vacances , et ca fait deux jours que je passe a bloquer complètement dessus , du coup je m'adresse a vous , en espérant que vous sauriez m'aider !
alors , voici l'énoncé :

u et v sont deux fonctions dérivables sur un intervalle I dont les dérivées u' et v' sont continues sur I.

1. Montrer que , pour tous nombres réels a et b de I ,
integr(b...a) u'(x)v(x)dx=[u(x)v(x)](b...a) - integr(b...a) u(x)v'(x)dx


--> Pour cette question je pense m'en être sortie , je l'ai fait a partir de (uv)'=u'v+uv'

2. On définit la suite (Kn) pour tout nombre entier naturel n non nul par
Kn=integr(1...0) (x^n)(e^-x)dx.

a) Calculer K1 à l'aide de la question 1.

pour cette question je bloque totalement , disons que j'arrive meme plus a calculer F(x) pour K1, je ne sais pas quelle formule utiliser .. ce qui m'empêche de répondre à la question si je comprend ?

ce qui fait que pour la suite , ca reste une totale catastrophe ..

b) démontrer que , pour tout n > ou égal a 1,
Kn+1 = -(1/e)+(n+1)Kn

c) calculer Ké et K".

d) en déduire la valeur de l'intégrale :
intergr(1...0) ((x^3)-(x^2)-x+1)e^-xdx


Je demande bien sure pas de réponse , mais des explications , de quoi me mettre sur la voie si possible ... Merci beaucoup !

Salut Nathalia,

et une petite intégration par parties (formule que tu as démontré à la question 1) fera l'affaire : Il te faut identifier entre et l'expression qui "jouera le rôle" de u'(x) et celle qui jouera celui de v(x). Tu identifies, tu trouves u(x) et v'(x) (une intégration et une dérivation simples), puis tu laisses tourner la formule.

[Ericovitchi]

Bonjour, donc tu veux calculer ?
Fait comme on te le suggère une intégration par parties en prenant u(x)=x et v'(x)=

[capitaine nuggets]

Salut !

2°)b) Raisonnement par récurrence.

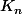2°)c) Tu connais en fonction de ainsi que le premier terme 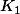donc, d'après la question précédente :
;
.

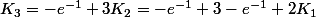2°)d) Remarque que :

.

:+++:

[nathalia33]

Salut Nathalia,

et une petite intégration par parties (formule que tu as démontré à la question 1) fera l'affaire : Il te faut identifier entre et l'expression qui "jouera le rôle" de u'(x) et celle qui jouera celui de v(x). Tu identifies, tu trouves u(x) et v'(x) (une intégration et une dérivation simples), puis tu laisses tourner la formule.

Merci de votre réponse , mais j'ai toujours un peu de mal .. Si par exemple je prend :
u'(x) = x
u(x) = (x^2)/2
et v(x) = e^-x
v'(x) = -e^-x
Je comprend toujours pas comment ca va m'aider a calculer K1 meme aprés l'avoir remplacer dans la formule ..

[Kikoo <3 Bieber]

Ça va le faire ;) Remplace dans ta formule et tu verras que cela fonctionnera !

[nathalia33]

Ça va le faire Remplace dans ta formule et tu verras que cela fonctionnera !

Non mais le probleme c'est que je ne sais pas si je dois me contenter de remplacer U et V dans ma formule , ou si j'ai d'autres calculs et notamment d'autres étapes a faire aprés , et si c'est le cas ( ce que je pense sinon ce serai trop facile non ? ) je n'arrive pas à identifier ces étapes..

[capitaine nuggets]

En posant et , on a et .
En effectuant une intégration par partie et d'après la formule :



on a :

.

Remarque : j'ai choisit de poser et au lieu de et car lorsque l'on effectuera l'intégration par partie, l'intégrale sera calculable.
Poser , ne ferait que nous compliquer la vie.

De manière général, lorsque l'on a :

avec un polynôme,
on posera et .
Poser où permettra d'avoir où .

Par exemple, tu peux calculer .
Sauf que là, il faudra effectuer deux intégrations par parties !

@+

[Kikoo <3 Bieber]

Tout à fait, et de manière générale, quand nous sommes exposés à un produit de fonctions, on privilégiera souvent de dériver le polynôme, en l'identifiant sous la fonction à dériver.

[nathalia33]

En posant et , on a et .
En effectuant une intégration par partie et d'après la formule :



on a :

.

Remarque : j'ai choisit de poser et au lieu de et car lorsque l'on effectuera l'intégration par partie, l'intégrale sera calculable.
Poser , ne ferait que nous compliquer la vie.

De manière général, lorsque l'on a :

avec un polynôme,
on posera et .
Poser où permettra d'avoir où .

Par exemple, tu peux calculer .
Sauf que là, il faudra effectuer deux intégrations par parties !

@+

D'accord , donc en fait une fois que j'ai , comme vous me l'avez dit , si je continue j'ai :

.
.

Ensuite , je calcule les expressions donc :

.

Ce qui fait que je trouve comme résultat :
.

C'est bien ça ?

[nathalia33]

Salut !

2°)b) Raisonnement par récurrence.

2°)c) Tu connais en fonction de ainsi que le premier terme donc, d'après la question précédente :
;
.

2°)d) Remarque que :

.

:+++:

Bonjour ! Alors j'avais aussi pensé au raisonnement par récurrence , mais je vois pas par où commencer .. J'avais pensé a comme normalement , démontrer a l'aide de la formule que avec Kn+1 = 1 , je trouve bien le résultat que j'ai calculé au a) , mais dans cette formule j'ai besoin de Kn, et pour Kn+1 = 1 j'ai n = 0 , or c'est pour n>1 ...