Aire maximale d'un rectangle

[bibiceboss]

Bonjour tout le monde, j'ai un DM a faire et je suis totalement bloqué.. Je n'y arrive pas..Voici l'énoncé:
Soit C un cercle de rayon r=1 et ABCD un rectangle inscrit dans C.
On pose AB=x et on note A(x) l'aire du rectangle ABCD correspondant.
On admet que, pour tout réel x de ]0;2[ : A(x)= x ;) 4-x^2
Determiner pour quelles valeur de x l'aire du rectangle ABCD est maximale et précisez la valeur de cette aire maximale

[chan79]

salut

Puisque l'aire est positive, cherche pour quelle valeur de x le carré de cette aire est maximal

(A(x))²=x²(4-x²)=...

[bibiceboss]

salut

Puisque l'aire est positive, cherche pour quelle valeur de x le carré de cette aire est maximal

(A(x))²=x²(4-x²)=...

Je ne suis pas sur d'avoir compris.. :/

[chan79]

Je ne suis pas sur d'avoir compris.. :/

Le carré de l'aire est

ou alors tu étudies la fonction qui donne l'aire en fonction de x

[bibiceboss]

Le carré de l'aire est

ou alors tu étudies la fonction qui donne l'aire en fonction de x

-(x^2 -2)^2 + (x^2 -2x)^2
C'est sa ?

[chan79]

-(x^2 -2)^2 + (x^2 -2x)^2
C'est sa ?

[bibiceboss]

Mais je ne comprends pas a quoi serre cette formule enfaite ? Et sur quoi on pourra aboutir avec sa ?

[chan79]

Mais je ne comprends pas a quoi serre cette formule enfaite ? Et sur quoi on pourra aboutir avec sa ?

le maximum pour le carré de l'aire est 4 (pour x²=2)

[bibiceboss]

le maximum pour le carré de l'aire est 4 (pour x²=2)

Comment sait-on sa ?

[chan79]

Comment sait-on sa ?

4-(x²-2)² c'est plus petit que 4 ( on ôte un nombre positif à 4)

[bibiceboss]

4-(x²-2)² c'est plus petit que 4 ( on ôte un nombre positif à 4)

Ah oui d'accord c'est vrai merci. Mais c'est tout ce qu'il fallait faire ?

[chan79]

Ah oui d'accord c'est vrai merci. Mais c'est tout ce qu'il fallait faire ?

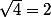
L'aire est maximale (donc pour )
Comme je l'ai mis plus haut, on pouvait aussi étudier la fonction A.

[bibiceboss]

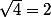
L'aire est maximale (donc pour )
Comme je l'ai mis plus haut, on pouvait aussi étudier la fonction A.

Est ce que vous pouvez me montrer et expliquer comment on fait avec la fonction de A juste pour savoir ?
Si sa ne vous dérange pas ?

[chan79]

Est ce que vous pouvez me montrer et expliquer comment on fait avec la fonction de A juste pour savoir ?
Si sa ne vous dérange pas ?

Etudie les variations de ( dérivée etc)

[bibiceboss]

Etudie les variations de ( dérivée etc)

A'(x)= 1x1/2;)4-x^2

[bibiceboss]

Ah non mince je me suis tromper: c'est sa plustôt:
;)(4-x²)+ x*1/2;)(4-x²)