Aide résolution système

[laubi]

Bonjour, j'ai besoin d'aide pour résoudre ce système

u''=f dans [0,1]
u(0)=0, u'(0)=a


et je dois démontrer que l'unique solution du système est:

u(x)= ax+integrale de 0 à x de( (x-t)*f(t)dt)

j'ai pensé à raisonner à l'envers mais je crois qu'il ne faut pas s'y prendre ainsi mais plutôt se ramener à un problème de cauchy.

Si quelqu'un a un idée, merci d'avance!!

Laura

[anima]

Bonjour, j'ai besoin d'aide pour résoudre ce système

u''=f dans [0,1]
u(0)=0, u'(0)=a


et je dois démontrer que l'unique solution du système est:

u(x)= ax+integrale de 0 à x de( (x-t)*f(t)dt)

j'ai pensé à raisonner à l'envers mais je crois qu'il ne faut pas s'y prendre ainsi mais plutôt se ramener à un problème de cauchy.

Si quelqu'un a un idée, merci d'avance!!

Laura

J'ai bien une idée pour le début; tu peux dire que si u'(0) est une constante (avec ou sans la dérivée d'une fonction, avec cette dérivée tendant vers zéro en zéro), alors u(0) = ax + une fonction + une constante d'intégration.
En gros, tu as
u'(0) = a + E(0) avec lim(x->0) E(0) = 0
Apres, Cauchy...je n'ai jamais étudié, pour etre honnete

[nico74]

Il s'agit de prouver tout d'abord que u vérifie E



u(x) vérifie bien les conditions de Cauchy :




De plus, d'après Leibniz



D'où


reste a prouver l'unicité

[nico74]

Unicité :

Supposons que u et v soient solutions de E, i.e. vérifient :

Pour tout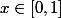 , u''(x)=f(x) et v''(x)=f(x);
et en plus u'(0)=v'(0)=a et u(0)=v(0)=0.

Donc pour tout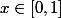 , u''(x)=v''(x).
En intégrant, on obtient u'(x)=v'(x)+C avec .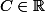

Or u'(0)=v'(0)=a d'où C=0.

Enfin, en intégrant de nouveau, u(x)=v(x)+D avec .

Mais comme u(0)=v(0)=0, on a D=0,

et donc Pour tout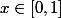 , u(x)=v(x).

D'où l'unicité

[nico74]

PS : le théorème de Leibniz que j ai utilisé :

Si
Alors,


Dans notre cas,

g(t,x)=(x-t)f(t), et

[nico74]

Oups je me suis emballé, tu es au lycée alors oublie ma solution