Aide en géométrie dans l'espace (TS)

[TS2502]

Bonsoir,
J'ai un exercice de maths à faire mais je ne vois pas comment y répondre. Votre aide me serait très utile

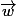
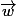
On donne les vecteurs (1;1;1), (2;7;-3) et (1;m;2). Comment faut-il choisir m tel que (O; ,, ) soit un repère de l'espace ?

J'ai vérifié que les vecteurs n'étaient pas colinéaires deux à deux (et donc non coplanaires) pour former alors une base de l'espace mais je ne vois pas comment définir m... J'ai pourtant essayé d'appliquer la formule de mon cours qui dit :
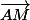
Si et non colinéaires et A appartenant à l'espace. Le plan est défini par = x + y

Malheureusement je n'y parviens pas... Merci de votre aide et de vos explications.

[pascal16]

m n'est pas unique.

il faut en effet que w ne soit pas dans le plan défini par u et v
mais attention le vecteur u+v n'est colinéaire ni avec u, ni avec v mais u,v et u+v ne définissent pas un repère de l'espace.

une façon basique :
1) u et v non liés
2) les vecteurs u,v et w sont liés s'il existe a et b tels que : au+bv=w
avec la première et 3ème coordonnées des vecteurs, je détermine a et b
ensuite je regarde ce que ça impose sur m, je trouve que
les vecteurs sont liés ssi m=0 (on a alors 7/5 u - 1/5 v =w )
donc les vecteurs ne sont pas liés ssi m est différent de 0

tu n'a pas vu le déterminant de vecteurs dans l'espace ?

[URemery]

Salut,

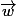
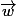
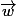
Les vecteurs ne sont en effet pas colinéaires deux à deux mais cela n'empêche pas que soit dans le plan porté par et ! C'est même le coeur du problême, si est dans ce plan, ils ne peuvent former une base de l'espace (puisqu'il est impossible de "sortir" de ce plan en combinant les vecteurs). Ils faut donc trouver pour que ne soit pas dans le
plan porté par et Tu comprends ?

[TS2502]

Merci de vos réponses.
Non je n'ai pas vu les déterminant de vecteurs dans l'espace ; qu'est-ce que c'est ?
Il faudrait donc que je vérifie pour quelle(s) valeur(s) de m on a :
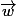
a + b ?

[pascal16]

oui c'est ça.

dans le plan, on dit que deux vecteurs A et B sont colinéaire si . est appelé le detérminant de A et B. Il existe une formule plus compliquée dans l'espace pour 3 vecteurs

[Lostounet]

Merci de vos réponses.
Non je n'ai pas vu les déterminant de vecteurs dans l'espace ; qu'est-ce que c'est ?
Il faudrait donc que je vérifie pour quelle(s) valeur(s) de m on a :
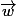
a + b ?

Oui,
Voici comment je procèderais.

Supposons que l'on puisse écrire le vecteur w en fonction de v et u, et regardons cela implique quoi pour la valeur possible de m (pour qu'ensuite on ne la choisisse pas...)

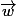
=a + b
Cela implique donc:



Cela te donne un système à 3 inconnues (en fait 2 inconnues et un paramètre ...), et tu peux trouver a et b. Cela te donner une seule valeur possible de m pour qu'effectivement on puisse écrire w comme combinaison linéaire des deux autres. Donc il faudra à tout prix ne pas choisir cette valeur de m.

Cela nous évite de parler explicitement de "déterminant" qui n'est pas au programme de TS.

[TS2502]

Cela me rappelle une formule de première pour la colinéarité il me semble... (pascal16)

En utilisant cette méthode, Lostounet, j'ai obtenu les mêmes valeurs que pascal16. Il me suffit donc de conclure que privé de 0 normalement (?)

[Lostounet]

Cela me rappelle une formule de première pour la colinéarité il me semble... (pascal16)

En utilisant cette méthode, Lostounet, j'ai obtenu les mêmes valeurs que pascal16. Il me suffit donc de conclure que privé de 0 normalement (?)

Bien vu: c'est la condition de colinéarité ! Et 0 est la valeur interdite pour m, j'ai trouvé pareil que toi.

[chan79]

Salut
On peut établir l'équation du plan vectoriel engendré par et .
On trouve facilement 2x-y-z=0
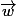
On remplace ensuite x, y et z par les coordonnées de et on a une équation en m qui donne la valeur interdite .