Point d'intesection de deux cercle
25 messages
- Page 1 sur 2 - 1, 2
point d'intesection de deux cercle
bonjour à tous,
svp je suis bloquée dans mon programme , je suis à la recherche des point dintersection de deux capteurs sans fil pour cela je dois résoudre un système d('equation du second degré de deux cercle comme chaque capteur est modélisé en cercle alors je dois creer des boucle pour parcourir chaque capteur et tester si sa distance avec son voisin est < rand de capture donc je calcule les points d'intesection mais le pb je dois retrouver une formule génerale de calcul de ces points j'ai trouvé sur intenet un PDF de la solution en générale mais elle est fausse SVP qlq poura m'aider je serai trés trés reconnaissante je suis bloquée svp :mur:
au fait le systeme d'équation est :
(x-xa)2+ (y-ya)2 =R2 tel que (xa,ya) le centre du cercle A
(x-xb)2+ (y-yb)2 = R2 (xb,yb)le centre du cerle B
svp je suis bloquée dans mon programme , je suis à la recherche des point dintersection de deux capteurs sans fil pour cela je dois résoudre un système d('equation du second degré de deux cercle comme chaque capteur est modélisé en cercle alors je dois creer des boucle pour parcourir chaque capteur et tester si sa distance avec son voisin est < rand de capture donc je calcule les points d'intesection mais le pb je dois retrouver une formule génerale de calcul de ces points j'ai trouvé sur intenet un PDF de la solution en générale mais elle est fausse SVP qlq poura m'aider je serai trés trés reconnaissante je suis bloquée svp :mur:
au fait le systeme d'équation est :
(x-xa)2+ (y-ya)2 =R2 tel que (xa,ya) le centre du cercle A
(x-xb)2+ (y-yb)2 = R2 (xb,yb)le centre du cerle B
Bonjour,
En reprenant deux équations de cercles quelconques :
(x - xa)² + (y - ya)² =RA²
(x - xb)² + (y - yb)² = RB²
x² - 2xxa + xa² + y² - 2yya + ya² = RA² (L1)
x² - 2xxb + xb² + y² - 2yyb + yb² = RB² (L2)
(L1) - (L2) :
RB² - RA² = xb² - xa² + 2x(xb - xa) + yb² - ya² + 2y(yb - ya)
RB² - RA² - xb² + xa² - 2x(xb - xa) - yb² + ya² = 2y(yb - ya)
} - x\frac{xb - xa}{yb - ya})
Posons :
})
Alors :
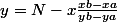
^2)
Donc en remplaçant y et y² par leur expression il vient :
^2 - 2(N - x\frac{xb - xa}{yb - ya})ya + ya^2)
Soit :
] + x [2(\frac{xb - xa}{yb - ya})ya - 2xa - 2Nx.\frac{xb - xa}{yb - ya}] + (xa^2 + ya^2 + N^2 - RA^2 - 2Nya) = 0)
Equation de la forma ax² + bx + c = 0
Il te suffit de calculer le discriminant et les racines, tu obtiendras 2 abscisses. Il te suffira de remplacer dans :
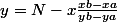
les valeurs de x pour trouver les ordonnées.
Formules non valable pour yb = ya mais les calculs deviennent beaucoup plus simple.
Essaye de reprendre le calcul avec cette démarche, cela te permettra dans ton programme d'avoir quelque chose du style :
Le programme sera alors très rapide et tu n'auras même pas à utiliser une boucle for =).
PS : Erreur incluses :zen:
En reprenant deux équations de cercles quelconques :
(x - xa)² + (y - ya)² =RA²
(x - xb)² + (y - yb)² = RB²
x² - 2xxa + xa² + y² - 2yya + ya² = RA² (L1)
x² - 2xxb + xb² + y² - 2yyb + yb² = RB² (L2)
(L1) - (L2) :
RB² - RA² = xb² - xa² + 2x(xb - xa) + yb² - ya² + 2y(yb - ya)
RB² - RA² - xb² + xa² - 2x(xb - xa) - yb² + ya² = 2y(yb - ya)
Posons :
Alors :
Donc en remplaçant y et y² par leur expression il vient :
Soit :
Equation de la forma ax² + bx + c = 0
Il te suffit de calculer le discriminant et les racines, tu obtiendras 2 abscisses. Il te suffira de remplacer dans :
les valeurs de x pour trouver les ordonnées.
Formules non valable pour yb = ya mais les calculs deviennent beaucoup plus simple.
Essaye de reprendre le calcul avec cette démarche, cela te permettra dans ton programme d'avoir quelque chose du style :
- Code: Tout sélectionner
Lecture pointA, pointB;
CalculerDiscriminant();
CalculerRacine();
AfficherPointIntersection();
Le programme sera alors très rapide et tu n'auras même pas à utiliser une boucle for =).
PS : Erreur incluses :zen:
Merci beaucoup, je vai essayé toute suite, mais la partie qui me fais peur bcp plus, c'est le delta, j'ai peur de tomber sur des solution negatif, et moi ma zone de deployement est positif donc je dois avoir tt les solution x, et y positif je ne sais pas si c'est moi qui se trempe a chaque fois dans le delta
merci merci merci , je reviendrai vers vous ca c sur :cry:
merci merci merci , je reviendrai vers vous ca c sur :cry:
sihem-manel a écrit:Merci beaucoup, je vai essayé toute suite, mais la partie qui me fais peur bcp plus, c'est le delta, j'ai peur de tomber sur des solution negatif, et moi ma zone de deployement est positif donc je dois avoir tt les solution x, et y positif je ne sais pas si c'est moi qui se trempe a chaque fois dans le delta
merci merci merci , je reviendrai vers vous ca c sur
On doit pouvoir faire quelque chose de plus simple avec changement de repère:
1) dans un repère avec origine en milieu de A et B et l'axe des X passant par A et B,

alors l'abscisse de l'intersection est 0
lordonnée est en racine( r²-(d/2)²) avec d distance des deux points
=> ce qui te donne au passage la condition d 0)
2) maintenant si tu reviens dans le repère initial
tu calcules les coordonnées du milieu
(xb-xa)/2 ; (yb-ya) /2
tu calcules le vecteur perpendiculaire au vecteur A B
( yb-ya; xa-xb)
tu le normes en divisant par racine((yb-ya)²+(xa-xb)² )
et tu le multiplie par racine( r²-(d/2)²)
et tu l'ajoutes au cooordonnée du mileu
[edit] ou tu le soustrais pour trouver le deuxième point d'intersection
Bonjour,
Il me semble avoir déjà vu évoquer ce même sujet, alors je vais faire la même réponse.
On a bien compris qu'il s'agit de vérifier et/ou compléter la position et la densité de capteurs.
La méthode adoptée est de calculer les différentes intersections de cercles entre eux, calculer les angles au centre, sommer ces différents angles et voir si les somme fait bien 360°.
Je crains qu'on soit dans le cas assez fréquent où on trouve la solution avant d'avoir posé le problème.
J'avais proposé une alternative qui consiste à utilisé la méthode de triangulation de Delaunay, ainsi les tests nécessaires ne portent que sur 3 points, et non pas chaque balise avec toutes les autres.
Il me semble avoir déjà vu évoquer ce même sujet, alors je vais faire la même réponse.
On a bien compris qu'il s'agit de vérifier et/ou compléter la position et la densité de capteurs.
La méthode adoptée est de calculer les différentes intersections de cercles entre eux, calculer les angles au centre, sommer ces différents angles et voir si les somme fait bien 360°.
Je crains qu'on soit dans le cas assez fréquent où on trouve la solution avant d'avoir posé le problème.
J'avais proposé une alternative qui consiste à utilisé la méthode de triangulation de Delaunay, ainsi les tests nécessaires ne portent que sur 3 points, et non pas chaque balise avec toutes les autres.
sihem-manel a écrit:j'ai besoin des valeurs de point d'intersection j'ai des valeurs negatif je compends pas prquoi svp
Salut, peux tu donner un exemple de coordonnées de A et de B , et de rayon qui te posent problème ?
Sinon n'oublie pas que dans un repère : trois quarts des points ont une coordonnée négative ....
Dlzlogic a écrit:J'avais proposé une alternative qui consiste à utilisé la méthode de triangulation de Delaunay, ainsi les tests nécessaires ne portent que sur 3 points, et non pas chaque balise avec toutes les autres.
Mon cher Dlz, on demande l'intersection de deux cercles ..... c'est tout .. ne complique pas, je veux dire essaie de comprendre les posts précédents ( dont le mien !!!) et propose une solution stp sans trop de barratins... le contexte est important mais les calculs aussi... merci
intesection de deux cercle
bonjour Dlzlogic
pour la phase des angles c'est fais et verifié et l'algorithme fonctionne tres bien, mais la maintenantt je dois resoudre un autre probleme , et de retrouver une formule génarale a implementer dans mon programme pour retrouver les points d'intesection de deux cercle svp aidez moi je suis bloquée ca fais une semaine je retrouve des resultats etonnant
merci bcp
pour la phase des angles c'est fais et verifié et l'algorithme fonctionne tres bien, mais la maintenantt je dois resoudre un autre probleme , et de retrouver une formule génarale a implementer dans mon programme pour retrouver les points d'intesection de deux cercle svp aidez moi je suis bloquée ca fais une semaine je retrouve des resultats etonnant
merci bcp
Pour calculer l'intersection de 2 cercles, après avoir vérifié qu'ils se coupent, c'est à dire d< 2*R, je calcule l'angle en A
alpha = acos(d/2*R) . Ceci est vrai dans ce cas particulier où les 2 rayons sont identiques. Sinon, c'est El Kachi (a² = b² + c² - 2bc cosA)
Le gisement de AB G=atan2(yB-yA, xB-xA)
XI1=xA + R*sin(G + alpha)
YI1=yA + R*cos(G + alpha)
XI2=xA + R*sin(G - alpha)
YI2=yA + R*cos(G - alpha)
Sauf erreur
alpha = acos(d/2*R) . Ceci est vrai dans ce cas particulier où les 2 rayons sont identiques. Sinon, c'est El Kachi (a² = b² + c² - 2bc cosA)
Le gisement de AB G=atan2(yB-yA, xB-xA)
XI1=xA + R*sin(G + alpha)
YI1=yA + R*cos(G + alpha)
XI2=xA + R*sin(G - alpha)
YI2=yA + R*cos(G - alpha)
Sauf erreur
et pour cette equation a² = b² + c² - 2bc cosA ???
donc avec ta méthode je n'est pa a chercher à résoudre les equation de cercle c'est ca ??? merci bcp pour vos reponse
donc avec ta méthode je n'est pa a chercher à résoudre les equation de cercle c'est ca ??? merci bcp pour vos reponse
Dlzlogic a écrit:J'ai conservé la notation de la figure de LeJeu.
A et B sont les centres des cercles.
Sauf erreur, ces formules ne nécessitent aucun contrôle de signe. La seule condition est celle du départ : la distance des centres est plus petite que 2 fois le rayon.
Ben oui,
On a les coordonnées de A et de B, et on a le rayon R.
On peut calculer la distance d entre A et B et puis tout le reste.
Oublie tout simplement qu'on pourrait aussi écrire l'équation des cercles, résoudre le système etc.
En tout cas c'est le méthode que j'utilise, et naturellement, je ne suis pas le seul, je n'ai rien inventé. Comme qui dirait, "c'est élémentaire".
C'est peut être "Al Kachi" qui te chagrine. Ca c'est dans le cas général, mais dans ton cas où les rayons des deux cercles sont égaux, c'est encore plus simple.
Tu fais un ou deux essais, si ça marche pas, tu reviens avec des valeurs numériques et je te montrerai.
On a les coordonnées de A et de B, et on a le rayon R.
On peut calculer la distance d entre A et B et puis tout le reste.
Oublie tout simplement qu'on pourrait aussi écrire l'équation des cercles, résoudre le système etc.
En tout cas c'est le méthode que j'utilise, et naturellement, je ne suis pas le seul, je n'ai rien inventé. Comme qui dirait, "c'est élémentaire".
C'est peut être "Al Kachi" qui te chagrine. Ca c'est dans le cas général, mais dans ton cas où les rayons des deux cercles sont égaux, c'est encore plus simple.
Tu fais un ou deux essais, si ça marche pas, tu reviens avec des valeurs numériques et je te montrerai.
Merci bcp Dlzlogic pour ta réponse qui etais tres tres clair, stp je reviens vers toi wallah je suis perdu et je dois soutenir ca c'est mon deuxieme prg à implémenter par exemple je prend ces capteirs ayant les positions suivantes:
je suis le noeud : 0 ma table de voisinage :
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 1 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 2 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 3 ma table de voisinage :
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 4 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
si je prend par exemple le capteur 2 et je veux calculer les points d'intesection: voila ce que j'ai mls:
if (dist < range)
{
alpha=(acos(dist/range)); //* 180 / 3.14;
G= atan (voisins[i].pos.y - posa.y)/(voisins[i].pos.x - posa.x); // * 180 / 3.14;
x1= posa.x + (range * sin (G + alpha)); //* 180 / 3.14); << je ne sais pas si je dois multiplier par 180 et diviser par P>>
y1=posa.y + ( range * cos(G + alpha)); //* 180 / 3.14);
x2= posa.x + (range * sin (G - alpha)); //* 180 / 3.14);
y2=posa.y + ( range * cos(G - alpha)); //* 180 / 3.14);
}
NS_LOG_INFO(" les point d'intesection du" << idf << "avec le voisin " << idf2 << "est" << x1 << "et " << y1 << "\n");
NS_LOG_INFO(" les point d'intesection du" << idf << "avec le voisin " << idf2 << "est " << x2 << "et " << y2 << "\n");
voila ce que j'ai comme resultat:
les point d'intesection du2 avec le voisin 0 est 21.8742 et 26.5179
20s les point d'intesection du2 avec le voisin 0 est 8.21223 et 29.0608
20s les point d'intesection du2 avec le voisin 1 est 27.3834 et 12.1192
20s les point d'intesection du2 avec le voisin 1 est 1.27583 et 24.5448
20s les point d'intesection du2 avec le voisin 3 est 21.2907 et 26.9536
20s les point d'intesection du2 avec le voisin 3 est -0.132798 et 22.6325
mais je pense que ces valeurs sont un peu bizar non , pouvez vous m'aider allah yestrek
je suis le noeud : 0 ma table de voisinage :
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 1 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 2 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 3 ma table de voisinage :
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 4 position_voisin : ( 15.773 , 13.992 ) |
je suis le noeud : 4 ma table de voisinage :
| id_voisin : 0 position_voisin : ( 4.586 , 4.121 ) |
| id_voisin : 1 position_voisin : ( 9.828 , 11.845 ) |
| id_voisin : 2 position_voisin : ( 12.61 , 14.72 ) |
| id_voisin : 3 position_voisin : ( 15.46 , 24.592 ) |
si je prend par exemple le capteur 2 et je veux calculer les points d'intesection: voila ce que j'ai mls:
if (dist < range)
{
alpha=(acos(dist/range)); //* 180 / 3.14;
G= atan (voisins[i].pos.y - posa.y)/(voisins[i].pos.x - posa.x); // * 180 / 3.14;
x1= posa.x + (range * sin (G + alpha)); //* 180 / 3.14); << je ne sais pas si je dois multiplier par 180 et diviser par P>>
y1=posa.y + ( range * cos(G + alpha)); //* 180 / 3.14);
x2= posa.x + (range * sin (G - alpha)); //* 180 / 3.14);
y2=posa.y + ( range * cos(G - alpha)); //* 180 / 3.14);
}
NS_LOG_INFO(" les point d'intesection du" << idf << "avec le voisin " << idf2 << "est" << x1 << "et " << y1 << "\n");
NS_LOG_INFO(" les point d'intesection du" << idf << "avec le voisin " << idf2 << "est " << x2 << "et " << y2 << "\n");
voila ce que j'ai comme resultat:
les point d'intesection du2 avec le voisin 0 est 21.8742 et 26.5179
20s les point d'intesection du2 avec le voisin 0 est 8.21223 et 29.0608
20s les point d'intesection du2 avec le voisin 1 est 27.3834 et 12.1192
20s les point d'intesection du2 avec le voisin 1 est 1.27583 et 24.5448
20s les point d'intesection du2 avec le voisin 3 est 21.2907 et 26.9536
20s les point d'intesection du2 avec le voisin 3 est -0.132798 et 22.6325
mais je pense que ces valeurs sont un peu bizar non , pouvez vous m'aider allah yestrek
Je peux mettre mon grain de sel ?
les données : centres des cercles) et
et ) , rayons des cercles R.
, rayons des cercles R.
Quitte à faire une petite translation, j'ai supposé = (0,0)) : ça ne coûte pas grand chose, et ça allège considérablement les formules !
: ça ne coûte pas grand chose, et ça allège considérablement les formules !
A la seule condition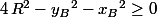 , les deux points d'intersection sont (x1, y1) et (x2, y2) donnés par les formules suivantes
, les deux points d'intersection sont (x1, y1) et (x2, y2) donnés par les formules suivantes
 \left(4\,{R}^{2} -{y_{{B}}}^{2}-{x_{<br />{B}}}^{2} \right) }}{{x_{{B}}}^{2}+{y_{{B}}}^{2}}})
 \left(4\,{R}^{2}- {y_{{B}}}^{2}-{x_<br />{{B}}}^{2} \right) }}{{x_{{B}}}^{2}+{y_{{B}}}^{2}}})
 \left(4\,{R}^{2} -{y_{{B}}}^{2}-{x_{<br />{B}}}^{2} \right) }}{{x_{{B}}}^{2}+{y_{{B}}}^{2}}})
 \left(4\,{R}^{2}- {y_{{B}}}^{2}-{x_<br />{{B}}}^{2} \right) }}{{x_{{B}}}^{2}+{y_{{B}}}^{2}}})
les données : centres des cercles
Quitte à faire une petite translation, j'ai supposé
A la seule condition
Je peux mettre mon grain de sel ?
les données : centres des cercles) et
et ) , rayons des cercles R.
, rayons des cercles R.
A la seule condition d'existence^{2} \geq (x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}) ,
,
les deux points d'intersection (x1, y1) et (x2, y2) sont donnés par les formules suivantes
^{2}+(y_{B}-y_A)^{2} } -\frac14}) : là, division et racine carrée sont assurées ! :zen:
: là, division et racine carrée sont assurées ! :zen:
/2 \ + \ (y_B-y_A) z)
/2 \ - \ (x_B-x_A) z)
/2 \ - \ (y_B-y_A) z)
/2 \ + \ (x_B-x_A) z)
C'est finalement simple ! Etonnant je trouve.
les données : centres des cercles
A la seule condition d'existence
les deux points d'intersection (x1, y1) et (x2, y2) sont donnés par les formules suivantes
C'est finalement simple ! Etonnant je trouve.
leon1789 a écrit:Je peux mettre mon grain de sel ?
les données : centres des cercleset
, rayons des cercles R.
A la seule condition d'existence,
les deux points d'intersection (x1, y1) et (x2, y2) sont donnés par les formules suivantes: là, division et racine carrée sont assurées ! :zen:
C'est finalement simple ! Etonnant je trouve.
Oui Léon, c'est particulièrement simple, on n'a pas besoin de trigo : ni de acos , ni de tan !
Mais si tu veux bien je proposais cette solution dans mon post précédent .....
mais l'important est bien de trouver le même résultat !
Bonjour Sihem-malen,
D'abord, pour les angles,
1- il est indispensable d'utiliser atan2(y,x) au lieu de atan(y/x), à moins de faire une fonction qui effectue la division "plus petit" divisé par "plus grand".
2- dans le cas présent vous n'avez pas à vous préoccuper de l'unité d'angle (radians ou degré), puisque la machine sait avec quelle unité d'angle elle travaille et gardera son unité d'angle, le radian en l'occurrence, mais vous n'êtes pas obligée de le savoir.
3- je ne vois pas en quoi ces valeurs peuvent paraitre bizarres.
Par contre , il y une chose qui me parait bizarre, je n'ai pas réussi à deviner le rayon des cercles.
Donnez les valeurs pour un seul couple de cercles,
Cercle A : X=.... Y=.... R=....
Cercle B : X=.... Y=.... R=....
Et les valeurs que vous trouvez
Point 1 X=.... Y=....
Point 2 X=.... Y=....
Je suppose que les valeurs sont en Km.
D'abord, pour les angles,
1- il est indispensable d'utiliser atan2(y,x) au lieu de atan(y/x), à moins de faire une fonction qui effectue la division "plus petit" divisé par "plus grand".
2- dans le cas présent vous n'avez pas à vous préoccuper de l'unité d'angle (radians ou degré), puisque la machine sait avec quelle unité d'angle elle travaille et gardera son unité d'angle, le radian en l'occurrence, mais vous n'êtes pas obligée de le savoir.
3- je ne vois pas en quoi ces valeurs peuvent paraitre bizarres.
Par contre , il y une chose qui me parait bizarre, je n'ai pas réussi à deviner le rayon des cercles.
Donnez les valeurs pour un seul couple de cercles,
Cercle A : X=.... Y=.... R=....
Cercle B : X=.... Y=.... R=....
Et les valeurs que vous trouvez
Point 1 X=.... Y=....
Point 2 X=.... Y=....
Je suppose que les valeurs sont en Km.
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
