Jacob Bernoulli somme des i exposant p jusqu a n
Discutez d'informatique ici !

-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
 par ortollj » 19 Oct 2019, 15:14
par ortollj » 19 Oct 2019, 15:14
Bonjour
quand j’ai regarde le
tableau de Jacob Bernoulli sur les
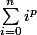
, j’etais scotché, je me demandais comment il a pu trouver ca.
Mais apres avec un peu de reflexion j’ai trouvé une des demonstrations super simple ! Tout ce dont on a besoin c’est uniquement des quatres operations, addition soustraction, multiplication et division.
je pense q'un eleve du secondaire peut tres bien comprendre et meme trouver lui meme cette demonstration .
Pour generer le Latex ci dessous, j’ai ecris un petit programme (obsolete, Python 2), voir nouveau lien Python 3 en derniere ligne
programme SageMath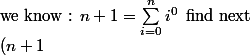}^{2} = {\sum_{i=0}^{n} {\left(i + 1\right)}^{2}} - {\sum_{i=0}^{n} i^{2}} \\ {\left(n + 1\right)}^{2} = {\sum_{i=0}^{n} i^{2} + 2 \, i + 1} - {\sum_{i=0}^{n} i^{2}} \\{\left(n + 1\right)}^{2} - {\sum_{i=0}^{n} 1} = 2 \, {\sum_{i=0}^{n} i} \\\frac{1}{2} \, {\left(n + 1\right)}^{2} - \frac{1}{2} \, {\sum_{i=0}^{n} 1} = {\sum_{i=0}^{n} i} \\\frac{1}{2} \, {\left(n + 1\right)}^{2} - \frac{1}{2} \, n - \frac{1}{2} = {\sum_{i=0}^{n} i} \\\frac{1}{2} \, n^{2} + \frac{1}{2} \, n = {\sum_{i=0}^{n} i} \\\text{we know : } \frac{1}{2} \, n^{2} + \frac{1}{2} \, n = \sum_{i=0}^{n}{i^{ 1 }} \, \text{ find next} \\{\left(n + 1\right)}^{3} = {\sum_{i=0}^{n} {\left(i + 1\right)}^{3}} - {\sum_{i=0}^{n} i^{3}} \\{\left(n + 1\right)}^{3} = {\sum_{i=0}^{n} i^{3} + 3 \, i^{2} + 3 \, i + 1} - {\sum_{i=0}^{n} i^{3}} \\{\left(n + 1\right)}^{3} - {\sum_{i=0}^{n} 1} - 3 \, {\sum_{i=0}^{n} i} = 3 \, {\sum_{i=0}^{n} i^{2}} \\\frac{1}{3} \, {\left(n + 1\right)}^{3} - \frac{1}{3} \, {\sum_{i=0}^{n} 1} - {\sum_{i=0}^{n} i} = {\sum_{i=0}^{n} i^{2}} \\\frac{1}{3} \, {\left(n + 1\right)}^{3} - \frac{1}{2} \, n^{2} - \frac{5}{6} \, n - \frac{1}{3} = {\sum_{i=0}^{n} i^{2}} \\\frac{1}{3} \, n^{3} + \frac{1}{2} \, n^{2} + \frac{1}{6} \, n = {\sum_{i=0}^{n} i^{2}} \\\text{we know : } \frac{1}{3} \, n^{3} + \frac{1}{2} \, n^{2} + \frac{1}{6} \, n = \sum_{i=0}^{n}{i^{ 2 }} \, \text{ find next} \\{\left(n + 1\right)}^{4} = {\sum_{i=0}^{n} {\left(i + 1\right)}^{4}} - {\sum_{i=0}^{n} i^{4}} \\{\left(n + 1\right)}^{4} = {\sum_{i=0}^{n} i^{4} + 4 \, i^{3} + 6 \, i^{2} + 4 \, i + 1} - {\sum_{i=0}^{n} i^{4}} \\{\left(n + 1\right)}^{4} - {\sum_{i=0}^{n} 1} - 6 \, {\sum_{i=0}^{n} i^{2}} - 4 \, {\sum_{i=0}^{n} i} = 4 \, {\sum_{i=0}^{n} i^{3}} \\\frac{1}{4} \, {\left(n + 1\right)}^{4} - \frac{1}{4} \, {\sum_{i=0}^{n} 1} - \frac{3}{2} \, {\sum_{i=0}^{n} i^{2}} - {\sum_{i=0}^{n} i} = {\sum_{i=0}^{n} i^{3}} \\\frac{1}{4} \, {\left(n + 1\right)}^{4} - \frac{1}{2} \, n^{3} - \frac{5}{4} \, n^{2} - n - \frac{1}{4} = {\sum_{i=0}^{n} i^{3}} \\\frac{1}{4} \, n^{4} + \frac{1}{2} \, n^{3} + \frac{1}{4} \, n^{2} = {\sum_{i=0}^{n} i^{3})
edited[ ci dessous adaptation du code Python 2 --> Python 3]
Code en Python 3 sur SageCellModifié en dernier par
ortollj le 14 Avr 2020, 08:08, modifié 1 fois.
si j'avais su j'aurais pas venu.
-
vladi
- Membre Relatif
- Messages: 179
- Enregistré le: 09 Sep 2019, 11:31
-
 par vladi » 23 Oct 2019, 00:06
par vladi » 23 Oct 2019, 00:06
ortollj a écrit:Bonjour
quand j’ai regarde le
tableau de Jacob Bernoulli sur les
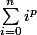
, j’etais scotché, je me demandais comment il a pu trouver ca.
Mais apres avec un peu de reflexion j’ai trouvé une des demonstrations super simple ! Tout ce dont on a besoin c’est uniquement des quatres operations, addition soustraction, multiplication et division.
Bonjour
En ce qui me concerne c'était en manipulant la formule du binôme de Newton que j'étais arrivé au coefficients de Bernoulli
(je ne suis pas dans la tête de Bernoulli mais à mon avis c'est comme ça que je suppose qu'il a fait)
à l'époque comme je ne connaissais pas ces coefficients je ne savais donc pas qu'ils étaient de lui
... des fois que si les quatre formules ci-dessous t'intéressent
avec la notation
)
pour les coefficients de Bernoulli
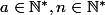
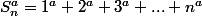
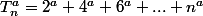
avec

est pair
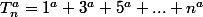
avec

est impair
ci-dessous ces deux formules
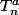
selon a est pair ou impair n'en font qu'une seule
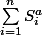
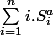
_________________
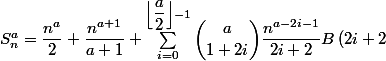)
________________
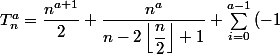^{i+a-2\left\lfloor\dfrac{a}{2}\right\rfloor }2^{a-i}\dbinom {a}{i}n^i S_{\left\lfloor\dfrac{n}{2}\right\rfloor }^{a-i})
________________
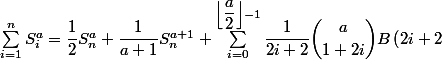 S_{n}^{a-2i-1})
________________
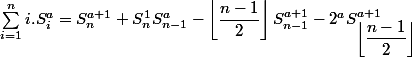
^n}{2} \left(n-1\right)^{a+1} + \displaystyle \sum _{i=1}^{\left\lfloor\dfrac{n-1}{2}\right\rfloor -1} S_{2i}^{a+1})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
