Fonction continue de Q dans R-Q et R-Q dans Q ?
14 messages
- Page 1 sur 1
Fonction continue de Q dans R-Q et R-Q dans Q ?
Bonjour,
je cherche à savoir s'il existe une fonction continue envoyant tout
rationnel sur un irrationnel et tout irrationnel sur un rationnel...
Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Pouvez vous me donner quelques indications, peut-être des petits lemmes
à montrer avant - ou c'est peut-être très simple ...
merci beaucoup d'avance
et je suis en mpsi
--
albert
je cherche à savoir s'il existe une fonction continue envoyant tout
rationnel sur un irrationnel et tout irrationnel sur un rationnel...
Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Pouvez vous me donner quelques indications, peut-être des petits lemmes
à montrer avant - ou c'est peut-être très simple ...
merci beaucoup d'avance
et je suis en mpsi
--
albert
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
Le théorème des valeurs intermédiaires et la densité de Q permettent de voir
que ça ne marche pas.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
Le théorème des valeurs intermédiaires et la densité de Q permettent de voir
que ça ne marche pas.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> > je cherche à savoir s'il existe une fonction continue envoyant tout[color=green]
> > rationnel sur un irrationnel et tout irrationnel sur un rationnel...
>
> Le théorème des valeurs intermédiaires et la densité de Q permettent de[/color]
voir
> que ça ne marche pas.
Je crois que je me suis emballé.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
> > rationnel sur un irrationnel et tout irrationnel sur un rationnel...
>
> Le théorème des valeurs intermédiaires et la densité de Q permettent de[/color]
voir
> que ça ne marche pas.
Je crois que je me suis emballé.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
albert junior , dans le message (fr.education.entraide.maths:59915), a
écrit :
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Il n'en existe pas. Enumère les rationnels: (r_n). Pour tout n,
f^{-1}({n}) est fermé, et inclus dans les irrationnels, donc d'intérieur
vide. Donc la réunion des f^{-1}({n}) et de tous les rationnels est, par
le théorème de Baire (google et tout et tout), d'intérieur vide, donc
contradiction puisque c'est R.
Yves, qui n'a pas le temps de plus détailler.
écrit :
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Il n'en existe pas. Enumère les rationnels: (r_n). Pour tout n,
f^{-1}({n}) est fermé, et inclus dans les irrationnels, donc d'intérieur
vide. Donc la réunion des f^{-1}({n}) et de tous les rationnels est, par
le théorème de Baire (google et tout et tout), d'intérieur vide, donc
contradiction puisque c'est R.
Yves, qui n'a pas le temps de plus détailler.
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> > > je cherche à savoir s'il existe une fonction continue envoyant tout[color=green][color=darkred]
> > > rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> >
> > Le théorème des valeurs intermédiaires et la densité de Q permettent de[/color]
> voir
> > que ça ne marche pas.
>
> Je crois que je me suis emballé.[/color]
Ah ben si en fait!
Soit f une telle application, et g définie par g(x)=f(x)-x. g est continue
et envoie tout réel sur un irrationnel (car la somme d'un rationnel et d'un
irrationnel est irrationnelle, ça se montre facilement par l'absurde).
Si g prenait deux valeurs distinctes u<v (des irrationnels, comme on vient
de le voir), et que w est un rationnel compris entre u et v, la valeur w
n'est pas prise par g (car w est rationnel), ce qui contredit le théorème
des valeurs intermédiaires. Donc g est constante: il existe un irrationnel a
tel que, pour tout x, g(x)=a, i.e. f(x)=x+a. Mais alors l'irrationnel a est
envoyé sur l'irrationnel 2*a, ce qui est absurde.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
> > > rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> >
> > Le théorème des valeurs intermédiaires et la densité de Q permettent de[/color]
> voir
> > que ça ne marche pas.
>
> Je crois que je me suis emballé.[/color]
Ah ben si en fait!
Soit f une telle application, et g définie par g(x)=f(x)-x. g est continue
et envoie tout réel sur un irrationnel (car la somme d'un rationnel et d'un
irrationnel est irrationnelle, ça se montre facilement par l'absurde).
Si g prenait deux valeurs distinctes u<v (des irrationnels, comme on vient
de le voir), et que w est un rationnel compris entre u et v, la valeur w
n'est pas prise par g (car w est rationnel), ce qui contredit le théorème
des valeurs intermédiaires. Donc g est constante: il existe un irrationnel a
tel que, pour tout x, g(x)=a, i.e. f(x)=x+a. Mais alors l'irrationnel a est
envoyé sur l'irrationnel 2*a, ce qui est absurde.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
Yves De Cornulier, dans le message (fr.education.entraide.maths:59918),
a écrit :
> Il n'en existe pas. Enumère les rationnels: (r_n). Pour tout n,
> f^{-1}({n}) est fermé, et inclus dans les irrationnels, donc d'intérieur
> vide. Donc la réunion des f^{-1}({n}) et de tous les rationnels est, par
> le théorème de Baire (google et tout et tout), d'intérieur vide, donc
> contradiction puisque c'est R.
[lire f^{-1}({r_n}) au lieu de f^{-1}({n}) - sorry]
a écrit :
> Il n'en existe pas. Enumère les rationnels: (r_n). Pour tout n,
> f^{-1}({n}) est fermé, et inclus dans les irrationnels, donc d'intérieur
> vide. Donc la réunion des f^{-1}({n}) et de tous les rationnels est, par
> le théorème de Baire (google et tout et tout), d'intérieur vide, donc
> contradiction puisque c'est R.
[lire f^{-1}({r_n}) au lieu de f^{-1}({n}) - sorry]
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
albert junior wrote:
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Avec la théorie de la mesure :
- l'image de Q par f est de mesure nulle,
- l'image de R\Q par f est inclus dans Q, donc de mesure nulle,
donc l'image de R par f est de mesure nulle.
Mais : si f n'est pas constante, il existe a < b qui appartiennent à
l'image de f. D'après le théorème des valeurs intermédiaires, [a,b]
appartient à l'image de f.
Mais [a,b] n'est pas de mesure nulle.
Par la contraposée, on en déduit que f est constante.
--
Benoît RIVET
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
Avec la théorie de la mesure :
- l'image de Q par f est de mesure nulle,
- l'image de R\Q par f est inclus dans Q, donc de mesure nulle,
donc l'image de R par f est de mesure nulle.
Mais : si f n'est pas constante, il existe a < b qui appartiennent à
l'image de f. D'après le théorème des valeurs intermédiaires, [a,b]
appartient à l'image de f.
Mais [a,b] n'est pas de mesure nulle.
Par la contraposée, on en déduit que f est constante.
--
Benoît RIVET
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
µ a écrit:
> Ah ben si en fait!
> Soit f une telle application, et g définie par g(x)=f(x)-x. g est continue
> et envoie tout réel sur un irrationnel (car la somme d'un rationnel et d'un
> irrationnel est irrationnelle, ça se montre facilement par l'absurde).
> Si g prenait deux valeurs distinctes u de le voir), et que w est un rationnel compris entre u et v, la valeur w
> n'est pas prise par g (car w est rationnel), ce qui contredit le théorème
> des valeurs intermédiaires. Donc g est constante: il existe un irrationnel a
> tel que, pour tout x, g(x)=a, i.e. f(x)=x+a. Mais alors l'irrationnel a est
> envoyé sur l'irrationnel 2*a, ce qui est absurde.
>
Bien vu !
Merci beaucoup
--
albert
> Ah ben si en fait!
> Soit f une telle application, et g définie par g(x)=f(x)-x. g est continue
> et envoie tout réel sur un irrationnel (car la somme d'un rationnel et d'un
> irrationnel est irrationnelle, ça se montre facilement par l'absurde).
> Si g prenait deux valeurs distinctes u de le voir), et que w est un rationnel compris entre u et v, la valeur w
> n'est pas prise par g (car w est rationnel), ce qui contredit le théorème
> des valeurs intermédiaires. Donc g est constante: il existe un irrationnel a
> tel que, pour tout x, g(x)=a, i.e. f(x)=x+a. Mais alors l'irrationnel a est
> envoyé sur l'irrationnel 2*a, ce qui est absurde.
>
Bien vu !
Merci beaucoup
--
albert
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
Benoit Rivet a écrit:
> Avec la théorie de la mesure :
> - l'image de Q par f est de mesure nulle,
> - l'image de R\Q par f est inclus dans Q, donc de mesure nulle,
>
> donc l'image de R par f est de mesure nulle.
>
> Mais : si f n'est pas constante, il existe a l'image de f. D'après le théorème des valeurs intermédiaires, [a,b]
> appartient à l'image de f.
>
> Mais [a,b] n'est pas de mesure nulle.
>
> Par la contraposée, on en déduit que f est constante.
>
Merci à toi et Yves pour vos réponses, mais il est plus simple pour moi
de prendre la démonstration de µ (je n'ai qu'une très petite idée des
notions que vous abordez ...)
--
albert
> Avec la théorie de la mesure :
> - l'image de Q par f est de mesure nulle,
> - l'image de R\Q par f est inclus dans Q, donc de mesure nulle,
>
> donc l'image de R par f est de mesure nulle.
>
> Mais : si f n'est pas constante, il existe a l'image de f. D'après le théorème des valeurs intermédiaires, [a,b]
> appartient à l'image de f.
>
> Mais [a,b] n'est pas de mesure nulle.
>
> Par la contraposée, on en déduit que f est constante.
>
Merci à toi et Yves pour vos réponses, mais il est plus simple pour moi
de prendre la démonstration de µ (je n'ai qu'une très petite idée des
notions que vous abordez ...)
--
albert
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> Merci à toi et Yves pour vos réponses, mais il est plus simple pour moi
> de prendre la démonstration de µ (je n'ai qu'une très petite idée des
> notions que vous abordez ...)
La démonstration d'Yves utilise les notions d'ouverts, de fermés, de
dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas des
réels, et le théorème de Baire qui en principe n'est pas au programme de
prépa mais est souvent vu en spé à titre d'exercice intéressant.
Quant à la théorie de la mesure, ça dépasse le cadre de la prépa, et bien
qu'intéressante je pense qu'il est un peu trop tôt en MPSI pour s'y coller
(il y a déjà assez de choses comme ça à découvrir).
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
> de prendre la démonstration de µ (je n'ai qu'une très petite idée des
> notions que vous abordez ...)
La démonstration d'Yves utilise les notions d'ouverts, de fermés, de
dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas des
réels, et le théorème de Baire qui en principe n'est pas au programme de
prépa mais est souvent vu en spé à titre d'exercice intéressant.
Quant à la théorie de la mesure, ça dépasse le cadre de la prépa, et bien
qu'intéressante je pense qu'il est un peu trop tôt en MPSI pour s'y coller
(il y a déjà assez de choses comme ça à découvrir).
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
µ a écrit:
> La démonstration d'Yves utilise les notions d'ouverts, de fermés, de
> dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas des
> réels, et le théorème de Baire qui en principe n'est pas au programme de
> prépa mais est souvent vu en spé à titre d'exercice intéressant.
Mmh j'ai un peu regardé sur google pour avoir une idée du théorème de
Baire, et ca me permets de comprendre le sens de la preuve d'Yves.
Après, je ne penses pas être en mesure de l'appliquer (ni que ce fut le
but de l'exo)... mais c'est sympa de voir ca
--
albert
> La démonstration d'Yves utilise les notions d'ouverts, de fermés, de
> dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas des
> réels, et le théorème de Baire qui en principe n'est pas au programme de
> prépa mais est souvent vu en spé à titre d'exercice intéressant.
Mmh j'ai un peu regardé sur google pour avoir une idée du théorème de
Baire, et ca me permets de comprendre le sens de la preuve d'Yves.
Après, je ne penses pas être en mesure de l'appliquer (ni que ce fut le
but de l'exo)... mais c'est sympa de voir ca
--
albert
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> > La démonstration d'Yves utilise les notions d'ouverts, de fermés, de[color=green]
> > dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas[/color]
des[color=green]
> > réels, et le théorème de Baire qui en principe n'est pas au programme de
> > prépa mais est souvent vu en spé à titre d'exercice intéressant.
>
> Mmh j'ai un peu regardé sur google pour avoir une idée du théorème de
> Baire, et ca me permets de comprendre le sens de la preuve d'Yves.
> Après, je ne penses pas être en mesure de l'appliquer (ni que ce fut le
> but de l'exo)... mais c'est sympa de voir ca[/color]
Il a des conséquences énormes qui dépssent le cadre de la prépa, je n'ai
d'ailleurs jamais compris pourquoi il n'était pas au programme de spé.
Garde-le sous le coude pour en reparler à ton prof quand tu seras en spé.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
> > dénombrabilité qui sont vues en spé mais pas très difficiles dans le cas[/color]
des[color=green]
> > réels, et le théorème de Baire qui en principe n'est pas au programme de
> > prépa mais est souvent vu en spé à titre d'exercice intéressant.
>
> Mmh j'ai un peu regardé sur google pour avoir une idée du théorème de
> Baire, et ca me permets de comprendre le sens de la preuve d'Yves.
> Après, je ne penses pas être en mesure de l'appliquer (ni que ce fut le
> but de l'exo)... mais c'est sympa de voir ca[/color]
Il a des conséquences énormes qui dépssent le cadre de la prépa, je n'ai
d'ailleurs jamais compris pourquoi il n'était pas au programme de spé.
Garde-le sous le coude pour en reparler à ton prof quand tu seras en spé.
--
µ
Doucement, n'est pas audible ni heures ni mouettes, docilement le coeur est
coupé
Re: Fonction continue de Q dans R-Q et R-Q dans Q ?
> je cherche à savoir s'il existe une fonction continue envoyant tout
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
>
Bon, au réveil et après la bataille, mais assez simple :
Il est possible de trouver un a rationnel tel que (0,f(0)) et (1,f(1))
soient de part et d'autre de y=ax.
D'après le théorème des valeurs intermédiaires (toujours lui), il existe
donc un x0 dans [0,1] tel que f(x0)=ax0, ce qui est évidemment impossible
d'après la définition de f.
CQFD
(En fait, l'idée de départ est de constater que f(x) ne peut couper aucune
droite y=ax avec a rationnel, ce qui montre bien la discontinuité de f).
> rationnel sur un irrationnel et tout irrationnel sur un rationnel...
> Après avoir pas mal cherché d'exemple je me résouds à penser qu'il n'en
> existe pas, mais je ne vois vraiment pas comment amorcer une preuve ...
>
Bon, au réveil et après la bataille, mais assez simple :
Il est possible de trouver un a rationnel tel que (0,f(0)) et (1,f(1))
soient de part et d'autre de y=ax.
D'après le théorème des valeurs intermédiaires (toujours lui), il existe
donc un x0 dans [0,1] tel que f(x0)=ax0, ce qui est évidemment impossible
d'après la définition de f.
CQFD
(En fait, l'idée de départ est de constater que f(x) ne peut couper aucune
droite y=ax avec a rationnel, ce qui montre bien la discontinuité de f).
Salut,
voici une preuve élémentaire reposant sur le théorème des valeurs intermédiaires (>) et qui me semble être préférable à l'utilisation du théorème de Baire dans ce cas, bien qu'elle utilise la dénombrabilité :
 est dénombrable donc
est dénombrable donc ) aussi.
aussi. ) est dénombrable car inclus dans
est dénombrable car inclus dans  . Ainsi,
. Ainsi, 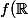) est dénombrable.
est dénombrable.
Le théorème des valeurs intermédiaires affirme que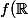) est un intervalle de
est un intervalle de  . Les seuls intervalles dénombrables de
. Les seuls intervalles dénombrables de  sont les singletons donc
sont les singletons donc  est constante, elle ne peut donc à la fois prendre des valeurs rationnelles et irrationnelles.
est constante, elle ne peut donc à la fois prendre des valeurs rationnelles et irrationnelles.
voici une preuve élémentaire reposant sur le théorème des valeurs intermédiaires (>) et qui me semble être préférable à l'utilisation du théorème de Baire dans ce cas, bien qu'elle utilise la dénombrabilité :
Le théorème des valeurs intermédiaires affirme que
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
