Tirage du loto

[Vassillia]

Bonjour, une petite question de proba pour faire une pause sur la géométrie.

Quelle est la probabilité qu'un tirage du loto présente au moins 2 nombres consécutifs ?
Vous avez le droit de répondre à l'intuition ou mieux par l'expérimentation
Toutefois, il y a au moins deux démonstrations assez différentes et assez abordables qui donnent la valeur exacte, à vous de choisir.

Rappel : Un tirage du loto est ensemble de 6 entiers distincts compris entre 1 et 49

[azf]

Bonjour Vassillia

Je déteste cette matière mais....ce que je sais c'est qu'il y en a autant que de faire 1-2-3-4-5-6-7

À moins que tu nous prouve que tu connais les relations entre deux tirages ...

Ceci dit avec GaBuZoMeu dans les parages j'ai appris à me méfier de mes délires

[azf]

super je doute déjà de ce que je viens de dire... (presque plus besoin de GaBuZoMeu là)

Qu'appelle tu Loto ? le jeu dans l'abstraction mathématique ou le vrai de la télé?

[Vassillia]

Merci pour ta participation azf mais tu fais bien de douter, cela m'étonnerait fortement que GaBuZoMeu soit d'accord avec toi. Le pauvre, il a vraiment vocation a être cité dans toutes les sales histoires sur les probas. Je ne pense pas qu'il y ait besoin de se méfier, c'est plûtot un avantage quand il prend le temps de rectifier les erreurs, enfin moi je le vis ainsi.

Bref, je parle du jeu où on tire sans remise des boules au hasard dans une urne et on regarde l'ensemble des boules obtenues (donc sans tenir compte de l'ordre). L'événement "tirage 1,2,3,4,5,6" est inclus dans l'événement "tirage avec au moins 2 nombres consécutifs" je suis d'accord mais c'est loin d'être le seul.
Pour moi, le "tirage 1,6,13,34,35,41" comporte aussi au moins 2 nombres consécutifs, n'est-ce pas azf ?

[azf]

et alors là je doute encore plus de ce que je viens de dire et je viens de me rendre compte que si Vassillia me reponds je vais passer pour un con lol

Elle ne sait pas que je suis archi nul en proba elle mais il faudrait le lui dire

[azf]

ah je vois qu'on a posté en même temps Vassillia

Oui ok tu as raison (en fait j'étais vraiment persuadé de ma première réponse et j'ai été de plus en plus méfiant jusqu'à l'extrême)

La prochaine fois je ferais attention

Merci Vassillia

[azf]

L'événement "tirage 1,2,3,4,5,6" est inclus dans l'événement "tirage avec au moins 2 nombres consécutifs"

La prochaine fois je vraiment faire attention

Bonne soirée Vassillia

[Vassillia]

Je vais essayer de te réconcilier avec les probas azf et je te rassure, tu ne pourras jamais faire pire que notre nemesis des mathématiciens et puis surtout, on est là pour apprendre.
Je te propose de calculer la probabilité d'avoir le "tirage 1,2,3,4,5,6" dont tu parlais, ce sera utile indirectement pour la suite de toute façon.
Bonne nuit.

[azf]

Merci Vassillia

Je sais que je vais me planter mais bon

ce sont des tirages de six

il y a tirages différents possibles

à mon avis c'est une chance sur

mais contrairement à tout à l'heure (au premier post) je suis de plus en plus certain que je vais me tromper

de toute façon ici sur ce forum vous êtes tous gentils (vous n'allez pas m'engueuler si je me trompe dans un calcul)

Par contre regarde là >>> (et c'est juste un commencement -on a encore rien vu)

c'était le 10 juillet https://www.youtube.com/watch?v=3Zuj1EHkWKI
moi je suis sicilien (je connais bien ces choses là)
c'était comme ça là-bas pendant la grande période des années 80
moi j'aimais bien Toto Riina mais bon un homme politique c'est plus class
Toto Riina ne portait pas de cravate mais il savait compter (c'est clair c'était l'homme le plus riche de toute la Sicile)

[GaBuZoMeu]

Bonjour,

On peut plutôt compter les tirages qui ne contiennent pas deux nombres consécutifs.
Les six nombres du tirage délimitent sept "tiroirs" (sept intervalles), dans la suite ordonnée des nombres et on peut se demander combien il y a de façons de ranger 49-6=43 chaussettes indiscernables dans 7 tiroirs, de façon à ce que les cinq tiroirs qui ne sont pas aux extrémités contiennent chacun au moins une chaussette. Du coup, on met 5 chaussettes de côté pour assurer cela, et on répartit comme on veut les 38 chaussettes restantes dans les 7 tiroirs.

[Vassillia]

Tu as parfaitement raison azf et tu viens de calculer le nombre total de tirages possibles qui va nous servir par la suite.
Merci pour la démonstration directe GaBuZoMeu, c'est la plus jolie je trouve. On peut aussi calculer le nombre de tirages sans nombre consécutif par récurrence si on sépare le cas où on tire la boule numérotée n+1 ou non.

Qui se dévoue pour conclure sur la probabilité recherchée ? Sa valeur numérique est relativement étonnante.

[Vassillia]

Bon, ben je me dévoue alors, en même temps c'est mon exercice c'est normal.
On doit répartir 38 chaussettes dans 7 tiroirs, cela revient à créer 6 séparateurs pour diviser la liste des 38 chaussettes.
Il y a 39 places possibles pour le premier séparateur (il faut compter une place avant toutes les chaussettes et une place après toutes les chaussettes)
Puis 40 places possibles pour le second séparateur (si on veut séparer au même endroit que précédemment, on peut le mettre juste avant ou juste après le premier séparateur)
Puis 41 places possibles pour le troisième séparateur
...
On trouve donc 39x40x41x42x43x44 places pour les séparateurs en tenant compte de l'ordre.
Problème, j'ai compté plusieurs fois les mêmes configurations car peu importe l'ordre dans lequel je mets les séparateurs donc on divise par 6!
On retrouve donc

La probabilité recherchée est donc il y a donc environ 1 chance sur 2 d'avoir des entiers consécutifs dans un tirage du loto, étonnant, non ?

[beagle]

étonnant? Je ne sais pas.
Un très incomplet estimateur basé sur 1 - pas consécutif

pas consécutif "grossier":
49/49 * 46/48 * 43/47 *40/46 * 37/45 * 34/44 = 0,48

(il manque les cas où il ya déjà écart de 1 entre deux numéros et les extrémités)

[Vassillia]

C'est un estimateur pas si mal, j'imagine que tu supprimes la boule que l'on vient de choisir puis la suivante et la précédente dans l'ordre de numérotation. Le calcul exact donne 44/49 * 43/48 * 42/47 * 41/46 * 40/45 * 39/44 = 0,505

Comment le justifier avec un support visuel comme tu aimes ? J'essaye autrement mais je ne te promets rien
On peut ordonner les boules et considérer qu'on les choisit dans l'ordre, dès qu'on tire une boule, on applique -1 a toutes les boules suivantes avant le prochain tirage pour s'assurer de ne pas avoir d'entiers consécutifs.
Au final, on va appliquer 5 fois -1 donc on va supprimer 5 boules qui seront interdites ce qui revient à choisir 6 boules parmi 49-5=44, on retrouve encore le même numérateur que précédemment

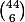
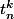
Sinon on peut aussi faire une récurrence qui se rapproche un peu plus de la méthode séquentielle déjà, on pose le nombre de tirages de k boules sans entiers consécutifs parmi n boules.
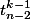
-Si on tire la boule n alors le nombre de tirages vérifiant la propriété est car on a pas le droit à la boule n-1 sinon c'est consécutif et on a déjà tiré une boule
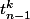
-Si on ne tire pas la boule n alors le nombre de tirages vérifiant la propriété est car on peut prendre la boule n-1 et on n'a pas encore tiré de boule.
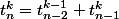
Au final avec l'initialisation et le triangle de Pascal, on s'en sort mais c'est plus laborieux je trouve.

[azf]

Merci Vassilia & GaBuZoMeu pour vos explications & Beagle pour le calcul en parallèle

j'avoue que j'ai passé plusieurs jours à être un peu paumé avec ces histoires de "chaussettes" mais bon je connais ça
La fameuse chaussette qui disparait collée au fond du tambour de la machine, je me suis perdu dedans pour la retrouver