J'ai fait un petit code c++ qui calcule les N premiers terme de la suite de Cesaro Cantor
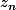
associée à une suite

arbitraire, par exemple dont les termes sont des nombres aléatoires entre 1 et 100.
On observe une convergence très rapide de
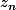
vers

Remarques :
- La complexité du calcul de
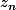
est en
)
, je ne pense pas qu'on puisse faire mieux.
- C'est sûrement mal optimisé en mémoire (d'ailleurs j'avais des bugs d'allocation mémoire)
- On peut facilement changer le code de Cesaro pour faire des poids variables
- Si on part d'une suite U=(1,0,0,...) on accède à
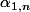
.
Voici la sortie d'une exécution typique
i: 0 U[i]: 84 Z[i] :84
i: 1 U[i]: 87 Z[i] :85.5
i: 2 U[i]: 78 Z[i] :84.1667
i: 3 U[i]: 16 Z[i] :83.151
i: 4 U[i]: 94 Z[i] :83.5949
i: 5 U[i]: 36 Z[i] :83.8585
i: 6 U[i]: 87 Z[i] :83.9828
i: 7 U[i]: 93 Z[i] :84.026
i: 8 U[i]: 50 Z[i] :84.0327
i: 9 U[i]: 22 Z[i] :84.0267
i: 10 U[i]: 63 Z[i] :84.0185
i: 11 U[i]: 28 Z[i] :84.0117
i: 12 U[i]: 91 Z[i] :84.0071
i: 13 U[i]: 60 Z[i] :84.0041
i: 14 U[i]: 64 Z[i] :84.0023
i: 15 U[i]: 27 Z[i] :84.0013
i: 16 U[i]: 41 Z[i] :84.0007
i: 17 U[i]: 27 Z[i] :84.0004
i: 18 U[i]: 73 Z[i] :84.0002
i: 19 U[i]: 37 Z[i] :84.0001
i: 20 U[i]: 12 Z[i] :84.0001
i: 21 U[i]: 69 Z[i] :84
i: 22 U[i]: 68 Z[i] :84
i: 23 U[i]: 30 Z[i] :84
i: 24 U[i]: 83 Z[i] :84
i: 25 U[i]: 31 Z[i] :84
i: 26 U[i]: 63 Z[i] :84
i: 27 U[i]: 24 Z[i] :84
i: 28 U[i]: 68 Z[i] :84
i: 29 U[i]: 36 Z[i] :84
i: 30 U[i]: 30 Z[i] :84
- Code: Tout sélectionner
#include
#include
#include
#include
using namespace std;
// sommation de Cesaro cantor
void cesaro(double *U, double *V,int N) // calcule les N premiers termes de la suite de Cesaro, et les stocke dans V
{
for(int i=0; i<N; i++) // initialise V[i]
{
V[i]=0;
}
for(int i=0; i<N; i++) // calcule V[i]
{
for(int j=0; j<i+1; j++) // somme pondérée des j premiers termes de U
{
V[i]+=1./(i+1)*U[j];
}
}
}
void cesaro_cantor(double *U, double *V,int N) // calcule les N premiers termes de la suite de Cesaro Cantor de U, et les stocke dans V
{
// déclaration
double *A=new double[N*N]; // stocke les N premiers termes des N-1 premiers itérés de Cesaro de U
double *B=new double[N]; // ligne courante de A;
double *D=new double[N]; // ligne suivante de A;
// initialisation
for(int i=0; i<N; i++)
{
B[i]=0;
D[i]=0;
for(int j=0;j<N;j++)
{
A[N*i+j]=0; // A[N*i+j] est le (j+1)ème terme du ième itéré de Cesaro de U.
}
}
for(int i=0; i<N; i++) // calcule le ième itéré de Cesaro de U (la ième ligne de A) en fonction des précédents
{
if(i==0)
{
std::cout << "Première ligne de A" << std::endl;
for(int j=0; j<N; j++)
{
A[j]=U[j]; // initialisation de la récurrence
std::cout << "j: "<< j << '\t' << "A[j]: " << A[j] << std::endl;
}
}
else
{
for(int j=0; j<N; j++)
{
A[j]=U[j]; // initialisation de la récurrence
std::cout << "j: "<< j << '\t' << "A[j]: " << A[j] << std::endl;
}
std::cout << "i: " << i << std::endl;
for(int j=0; j<N;j++)
{
std::cout << " A[i,j] " << A[N*(i-1)+j] << std::endl;
B[j]=A[N*(i-1)+j]; // ligne courante de A
}
cesaro(B, D, N); // calcul de la ligne suivante de A, hérédité
for(int j=0; j<N; j++)
{
std::cout << "j: "<< j << '\t' << "B[j]: " << B[j] << std::endl;
}
}
for(int j=0; j<N; j++) // recopie de la ligne suivante de A
{
A[i*N+j]=D[j];
}
}
for(int i=0; i<N; i++) // calcul de Zn, la suite de Cesaro Cantor de U
{
V[i]=A[i*N+i];
}
for(int i=0; i<N;i++)
{
for(int j=0; j<N; j++)
{
std::cout << A[i*N+j] << '\t';
}
std::cout << std::endl;
}
std::cout << std::endl;
}
int main()
{
int N=100;
double *U=new double[N];
double *V=new double[N];
for(int i=0; i<N; i++) // initialisation
{
U[i]=rand()%100+1;
V[i]=0;
}
cesaro_cantor(U,V,N); // calcul de V
// affichage
for(int i=0; i<N; i++)
{
std::cout << "i: " << i << '\t' << "U[i]: "<< U[i] << '\t' << "Z[i] :" << V[i] << std::endl;
}
return 0;
}
EDIT : j'ai linké la question ici
http://www.les-mathematiques.net/phorum/read.php?4,1031025,1031025#msg-1031025