Un satellite en orbite circulaire...
11 messages
- Page 1 sur 1
Un satellite en orbite circulaire...
Un satellite est en orbite circulaire de rayon 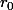 autour de la Terre. Montrer qu'en dessous d'une certaine valeur de
autour de la Terre. Montrer qu'en dessous d'une certaine valeur de 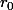 , le satellite se désagrège. :space:
, le satellite se désagrège. :space:
C'est bien la limite de roche, oui.
On prend un satellite sphérique de rayon et de masse
et de masse  .
.
Une distance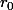 sépare le centre de la Terre et le centre du satellite. On estime que le satellite ne tourne pas sur soi-même.
sépare le centre de la Terre et le centre du satellite. On estime que le satellite ne tourne pas sur soi-même.
Maintenant, prenons les cas extrèmes. On considère 3 éléments de masse dm situés à la surface du satellite la plus proche-lointaine de la terre, et au centre du satellite.
La terre tire sur l'élément de masse du satellite qui lui est la plus proche avec une force valant
^2})
Et sur la face la plus lointaine avec une force valant
^2})
Le centre du satellite est lui tiré avec une force de
^2})
Donc, si l'on veut bien, le centre du satellite a l'impression que la face plus proche est tiré vers la terre, et que la face la plus lointaine est poussée dans la direction opposée (puisque le centre ressent une force supérieure à la face lointainte ). On peut s'en convaincre avec F_1 - F_2, et F3 - F_2.
On voit donc que le satellite, depuis son centre, se sent 'écartelé', c'est ce qu'on appelle la force de marrée.
Qu'est-ce qui le tient ensemble ? Sa propre force graviationnelle. la masse du satellite tire sur les échantillons dm avec une force

On considère seulement , car la face proche est tirée plus violamment loin du satellite (et par rapport au satellite, d'ou le
, car la face proche est tirée plus violamment loin du satellite (et par rapport au satellite, d'ou le  ) que l'extérieur, donc casse plus vite (au sens que c'est cette face qui impose la limite inférieure sur r_0). Il existe un r_0 tel que
) que l'extérieur, donc casse plus vite (au sens que c'est cette face qui impose la limite inférieure sur r_0). Il existe un r_0 tel que  , donc que la graviation propre du satellite n'est pas assez forte pour retenir l'élément de masse dm au bord du satellite. Boum, ça éclate.
, donc que la graviation propre du satellite n'est pas assez forte pour retenir l'élément de masse dm au bord du satellite. Boum, ça éclate.

^2} - GM_t dm \frac{1}{r_0}^2)
On approxime par r_s petit devant r_0

D'où
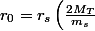^{1/3})
Et donc si on a à faire a des corps sphérique, on réduit à
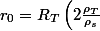^{1/3}) comme l'avait dit Zweig (ici ton K =
comme l'avait dit Zweig (ici ton K = 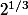 ).
).
D'autre approximations donnent d'autres constantes, mais celle-ci est assez simple.
A+
PS: Si c'était vraiment une olympiade, j'voudrais bien voir la gueule des réponses, parce que l'information 'orbite circulaire', c'est de la bonne intox.
On prend un satellite sphérique de rayon
Une distance
Maintenant, prenons les cas extrèmes. On considère 3 éléments de masse dm situés à la surface du satellite la plus proche-lointaine de la terre, et au centre du satellite.
La terre tire sur l'élément de masse du satellite qui lui est la plus proche avec une force valant
Et sur la face la plus lointaine avec une force valant
Le centre du satellite est lui tiré avec une force de
Donc, si l'on veut bien, le centre du satellite a l'impression que la face plus proche est tiré vers la terre, et que la face la plus lointaine est poussée dans la direction opposée (puisque le centre ressent une force supérieure à la face lointainte ). On peut s'en convaincre avec F_1 - F_2, et F3 - F_2.
On voit donc que le satellite, depuis son centre, se sent 'écartelé', c'est ce qu'on appelle la force de marrée.
Qu'est-ce qui le tient ensemble ? Sa propre force graviationnelle. la masse du satellite tire sur les échantillons dm avec une force
On considère seulement
On approxime par r_s petit devant r_0
D'où
Et donc si on a à faire a des corps sphérique, on réduit à
D'autre approximations donnent d'autres constantes, mais celle-ci est assez simple.
A+
PS: Si c'était vraiment une olympiade, j'voudrais bien voir la gueule des réponses, parce que l'information 'orbite circulaire', c'est de la bonne intox.
Zweig a écrit:Oui voilà, c'était racine cubique de 2 la fameuse constante !
C'pas vraiment une Olympiade en soi, ça a été donné à un oral d'Ulm ...
Je suis tombé là-dessus à mon oral d'astrophysique. J'avais vu la démo en cours et me souvenais des grandes lignes. Si par contre on a jamais vu (j'imagine qu'à Ulm ils aiment bien faire les sauvages) , c'est chaud de bien partir.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
