Relation valable pour tt a,b,c,d,e
Olympiades mathématiques, énigmes et défis
-
Alexa [Bot]
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Déc 2015, 16:13
-
 par Alexa [Bot] » 14 Aoû 2006, 10:50
par Alexa [Bot] » 14 Aoû 2006, 10:50
[mode troll on]

[mode troll off]
Igor, que désolé, c'était trop tentant *grin*.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2006, 11:50
par aviateurpilot » 14 Aoû 2006, 11:50
tu n'a pas trouvé la source igor car c'est moi qui a creé ce exo
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Aoû 2006, 11:55
par Nightmare » 14 Aoû 2006, 11:55
Attention Igor, tu vas être traité de con (Cf
ici )
:lol3:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2006, 12:30
par aviateurpilot » 14 Aoû 2006, 12:30
on veux trouver a,b,c,d,e

donne 0,0,0,0,1

donne 0,0,0,1,1

donne 0,0,1,1,1

donne 0,1,1,1,1

donne 1,1,1,1,1
soit (x,y,z,t,w) la solution de

on pend

cherche une autre expression
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 14 Aoû 2006, 13:20
par BiZi » 14 Aoû 2006, 13:20
aviateurpilot a écrit:on veux trouver a,b,c,d,e

cherche une autre expression
Plus généralement,
Si les premiers termes de la suite sont
U1=A1
U2=A2
....
Uk=Ak
Alors
Un=A1*E((n+k)/k+1))+A2*E((n+(k-1))/(k+1))+...+An*E((n+1)/(k+1))
Maintenant qu'on a une formule générale, il n'y'a plus aucun intérêt à poser des problèmes de suite de chiffres. On peut donc faire la paix avec Nightmare :ptdr:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2006, 13:31
par aviateurpilot » 14 Aoû 2006, 13:31
Si les premiers termes de la suite sont
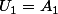
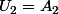
....
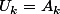
=0)
pour

et
=A_i)
pour
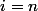
donc
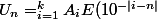=A_n)
pour n de {

}
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 14 Aoû 2006, 15:21
par Patastronch » 14 Aoû 2006, 15:21
[edit] j'ai rien dit je viens de comprendre.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités