Points imaginaires-Droite réelle

[hammana]

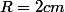
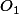
Soient un cercle de centre de rayon , et un cercle de centre de rayon
La distance .
Construire la droite passant par les points d'intersection des deux cercles. Cette droite coupe en un point H, mesurer OH puis le calculer et vérifier la concordance des résultats.

[hammana]

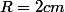
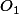
Soient un cercle de centre de rayon , et un cercle de centre de rayon
La distance .
Construire la droite passant par les points d'intersection des deux cercles. Cette droite coupe en un point H, mesurer OH puis le calculer et vérifier la concordance des résultats.

La question n'a pas l'air de susciter beaucoup d'intérêt. Voilà un petit coup de pouce:
Montrer que si les deux cercles se coupent en deux points réels M et N. La droite MN rencontre les tangentes communes aux deux cercles en leur milieu. C'est une propiété caractéristique de la droite qui reste valable quand on voit plus M et N.

[Dlzlogic]

Bonjour,
Si j'ai bien lu les hypothèses, les cercles ne se coupent pas.
Mais il est possible que vous cherchiez une approche des faisceaux de cercle.
Je pense que les faisceaux de droite sont une notion largement oubliée, alors, les faisceaux de cercle :cry:

[hammana]

Bonjour,
Si j'ai bien lu les hypothèses, les cercles ne se coupent pas.
Mais il est possible que vous cherchiez une approche des faisceaux de cercle.
Je pense que les faisceaux de droite sont une notion largement oubliée, alors, les faisceaux de cercle

Oui, on a dû laisser tomber une bonne partie de l'ancien pour faire place au nouveau.