Point fixe mobile ???

[Ben314]

Suite à une question posé sur un autre Forum, une petite colle d'analyse :

On se donne deux suites complexes et telle que :
1) La suite converge vers un complexe .
2) Il existe un réel tel que .

Devinez quelle est la question puis . . . y répondre . . .

[catamat]

Bonjour

Bon je m'y attelle puisque personne n'a rien proposé pour le moment...

Personnellement cela me rappelle mon cours sur les equa diff et les applications contractantes, mais bon j'ai bcp bcp oublié...

Je vais donc donner juste quelques remarques...
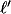
D'abord ne peut pas avoir une limite différente de , en effet la condition 2) donnerait une absurdité en passant à la limite.

On sait que a pour limite, donc à partir d'un certain rang N, la distance sera inférieure à un aussi petit que voulu.

D'autre part la condition 2) signifie que le point d'affixe sera plus près du point d'affixe que ne l'était le point d'affixe .

Donc se "rapproche" de qui lui même se "rapproche" de , on pourrait conjecturer que la suite a pour limite ...

Mais bon il faut démontrer que se "rapproche" de d'aussi près que voulu, pour le moment je n'y suis pas arrivé.

[Ben314]

Perso., je ne sais le faire qu'avec du "coupage de en rondelle".
Si personne ne trouve d'ici quelque temps, je mettrais une solution.

[catamat]

Bon, voilà où j'en suis... :

k est la constante donnée dans l'énoncé
Soit N tel que pour tout entier n supérieur à N on ait :

Soit un entier n supérieur à N



Or

D'où en combinant les deux résultats



On peut en déduire par récurrence (sauf erreur) que :



où

donc

ou

donc



Bon si je ne me suis pas gouré jusque là, on doit pouvoir majorer ceci par un nombre strictement positif aussi petit que voulu puisque 0<k<1 la limite du premier terme est nulle, quant au second le choix du peut le rendre aussi petit que voulu.

[Ben314]

Bravo !!
C'est ce que j'avais fait à un détail prés : quand tu as ta majoration tu peut directement majorer par vu que la différence ne risque pas de changer quoi que ce soit (dans une suite arithmético-géométrique ce terme ne joue que comme une constante multiplicative donc ou ça change rien).

Ca simplifie un peu la suite.

[catamat]

Super !
Merci pour cet exo qui m'a bien plu.

[Ben314]

J'ai absolument pas regardé (donc aussi bien ça déconne complet), mais dans le même style et en plus symétrique, on peut regarder ça :

On se donne deux suites complexes et et on suppose qu'il existe un réel tel que :
1) .
2) .

Est-ce que les deux suites sont forcément convergentes ?

[Ben314]

Cherche pas : ça ne marche pas du tout . . .
Si on prend avec où alors les conditions sont vérifiées sauf que la matrice en plus de la valeur propre (correspondant à ), elle a aussi comme valeur propre qui n'est pas forcément de module <1, même en imposant à d'être très proche de 0 (vu qu'on peut prendre qui donne réel <-1).