Plus petite multiple - Partie 2
Olympiades mathématiques, énigmes et défis
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 12:28
par alice02 » 16 Déc 2017, 12:28
Le plus petit nombre entier positif divisible par
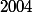
et s’écri-
vant en base dix avec les seuls chiffres

et

est
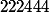
.
Quel est le suivant ?
(C'est un exercice sur les congruences, mais je ne sais pas comment les utiliser dans ce cas... )

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2017, 12:45
par Ben314 » 16 Déc 2017, 12:45
Salut
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 12:48
par alice02 » 16 Déc 2017, 12:48
Merci Ben314, mais quelle est la méthode pour trouver ce numéro?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2017, 13:15
par Ben314 » 16 Déc 2017, 13:15
On peut (éventuellement) commencer par tout diviser par deux, c'est à dire cherche les nombres N composés (leurs chiffres) uniquement de 1 et de 2 qui sont divisible par 1002, c'est à dire congru à 0 modulo 1002.
Or 1000=-2 mod 1002 donc si tu écrit N en base 1000 : N=a0+1000.a1+1000^2.a2+... (ce qui revient à regrouper les chiffres 3 par 3), modulo 1002 on a N congru à a0-2.a1+4.a2-8.a3+...
Donc il faut chercher des nombre a0,a1,... à 3 chiffres composé uniquement de 1 et de 2 (sauf le dernier qui peut commencer par des 0) tels que a0-2.a1+4.a2-8.a3+... = 0 modulo 1002.
La première solution (triviale) est a0=222 et a1=111.
La suivante est un peu plus compliquée à trouver, mais ça se fait : a0=122 ; a1=221 ; a2=122 ; a3=021
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
alice02
- Membre Naturel
- Messages: 56
- Enregistré le: 28 Aoû 2017, 16:28
-
 par alice02 » 16 Déc 2017, 13:21
par alice02 » 16 Déc 2017, 13:21
Une méthode intéressante, félicitations Ben314 !!

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités