Peano...

[Ben314]

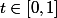
On part de la courbe paramétrée puis on construit de façon récursives les courbes en suivant le processus indiqué par le dessin çi dessus (toutes les courbes sont paramétrées pour et parcourues à vitesse constante).
Bien sûr, on peut :
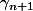
a) Donner une formule "calculatoire" pour en fonction de .
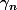
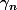
b) Vérifier que les courbes sont continues et qu'elles convergent uniformément vers une fonction
c) Montrer que est non seulement continue mais qu'elle remplie le carré.

Mais, les questions qui m'interessent sont plutôt :
d) Pouvez vous donner les coordonnées exactes du point ?
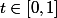
e) Déterminer le(s) tel(s) que ?

[Doraki]

je trouve ;)(2/15) = (1/3, 1/3) et ;)(455/816) = (3/5, 3/4)

[Ben314]

je trouve (2/15) = (1/3, 1/3) et (455/816) = (3/5, 3/4)

Pour être franc, je n'ai pas (encore) fait les calculs, mais il me semble bien qu'il y devrait y avoir une deuxième solution pour gamma(t)=(3/5, 3/4)...


Edit : aprés calculs, je trouve bien (2/15) = (1/3, 1/3)
Mais par contre, j'ai (447/816) = (463/816) = (3/5, 3/4)
Mais, ça dit pas comment faut faire...

Remarque : en fait, le truc rigolo, c'est que gamma envoie [0,1]nQ sur ([0,1]nQ)² et réciproquement.

[Doraki]

Ah ouais j'avais oublié 463/816.

Tiens j'vais essayer de dessiner à quoi ressemble la courbe quand on relie tous les ;)(k/d) pour d fixe et k allant de 0 à d.

[Ben314]

Tient, temp qu'à faire je rajoute deux questions un peu plus "rigolote" :

f) Quel est le nombre maximum d'antécédent d'un point (x,y) de [0,1]² ?
g) Pouvez vous caractériser les point (x,y) ayant exactement un antécédent ? exactement deux ? etc...