Bonjour, Quelqu'un pourrait-il m'expliquer "pas à pas" le calcul et résultat énoncé ci-dessous sur le nombre de combinaisons possibles sur le tableau de connexion de la machine Enigma ?
Le tableau de connexions*: à l'aide de 6 câbles, on relie 12 lettres deux-à-deux*; ainsi 12 lettres sont permutées et 14 d'entre elles restent inchangées, le nombre de combinaisons s'écrit donc /
;)
26!/12!x14! x 12!/6!x 2puissance6(64) = 100 391 791 500
Merci
Nombre combinaisons de la machine enigma
9 messages
- Page 1 sur 1
Salut,
Il y a (comme toujours) des tas de façons plus ou moins rapide de faire le calcul.
Perso, je pense que je ferais comme ça :
1) Choix des 12 lettres qui vont être connecté parmi les 26 :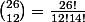 possibilités.
possibilités.
2) Je "dissymétrise" les câbles en considérant qu'ils ont une lettre "de départ" une lettre "d'arrivée".
Comme il y a deux "orientations" possible pour chaque câble, ça multiple par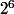 le nombre de possibilités : il faudra donc diviser le résultat obtenu par 2^6 pour avoir la bonne valeur.
le nombre de possibilités : il faudra donc diviser le résultat obtenu par 2^6 pour avoir la bonne valeur.
3) Choix des 6 lettre "de départ" parmi les 12 à connecter :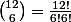 possibilités.
possibilités.
Résultat :^2})
Il y a (comme toujours) des tas de façons plus ou moins rapide de faire le calcul.
Perso, je pense que je ferais comme ça :
1) Choix des 12 lettres qui vont être connecté parmi les 26 :
2) Je "dissymétrise" les câbles en considérant qu'ils ont une lettre "de départ" une lettre "d'arrivée".
Comme il y a deux "orientations" possible pour chaque câble, ça multiple par
3) Choix des 6 lettre "de départ" parmi les 12 à connecter :
Résultat :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
je n'ai rien compris
Je suis désolé mais je ne comprends rien ! pas à pas, opération par opération ça dit quoi
Ben314 a écrit:Salut,
Il y a (comme toujours) des tas de façons plus ou moins rapide de faire le calcul.
Perso, je pense que je ferais comme ça :
1) Choix des 12 lettres qui vont être connecté parmi les 26 :possibilités.
2) Je "dissymétrise" les câbles en considérant qu'ils ont une lettre "de départ" une lettre "d'arrivée".
Comme il y a deux "orientations" possible pour chaque câble, ça multiple parle nombre de possibilités : il faudra donc diviser le résultat obtenu par 2^6 pour avoir la bonne valeur.
3) Choix des 6 lettre "de départ" parmi les 12 à connecter :possibilités.
Résultat :
bjr
Le nombre total de combinaisons :
158 962 555 217 826 360 000 = 1,59x10^20 combinaisons
voir dans la rubrique combinaisons la démo pour le calcul du nombre de combinaisons!
http://fr.wikipedia.org/wiki/Enigma_%28machine%29
Le nombre total de combinaisons :
158 962 555 217 826 360 000 = 1,59x10^20 combinaisons
voir dans la rubrique combinaisons la démo pour le calcul du nombre de combinaisons!
http://fr.wikipedia.org/wiki/Enigma_%28machine%29
WillyCagnes a écrit:bjr
Le nombre total de combinaisons :
158 962 555 217 826 360 000 = 1,59x10^20 combinaisons
http://fr.wikipedia.org/wiki/Enigma_%28machine%29
c'est la façon de trouver ce chiffre qui m'importe !
A+
Boullitt : si j'ai bien compris tu ne connais pas les méthodes de dénombrement (puisque tu ne sais pas ce que signifie le symbole « ! »). Il faut donc d'abord que tu lises un cours sur le sujet. Peut-être celui-ci : http://www.iecn.u-nancy.fr/~rmarchan/Enseignement/LicenceMI2/chap1.pdf (premier cours trouvé avec Google ; ici le dénombrement est présenté dans un cadre probabiliste ; à part le court §1.1 on est dans le sujet).
bonsoir et merci d'avoir pris la peine de comprendre mon souci. Je suis allée sur le lien que vous m'avez donné et essayé mais sans grand succès de comprendre le dénombrement.
Je pense qu'il faut déjà déterminer l'univers global (26 puissance 12 ??) et après ça beugue ( vue mon âge et mon niveau scolaire mais bon, il n'y a pas d'âge pour essayer de comprendre quelque chose) .
Merci de votre patience pour une explication détaillée
Je pense qu'il faut déjà déterminer l'univers global (26 puissance 12 ??) et après ça beugue ( vue mon âge et mon niveau scolaire mais bon, il n'y a pas d'âge pour essayer de comprendre quelque chose) .
Merci de votre patience pour une explication détaillée
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
