Les zéros Fibonacci

par **nodjim** » 22 Juil 2010, 17:00

Bonsoir à tous.
Un petit problème pas bien méchant.
On sait qu'un nombre de Fibonacci Fp de rang p premier est congru à 0 modulo p au rang p+1 ou p-1, si p différent de 5.
Qu'en est il alors de leurs multiples ?
Application: trouver le plus petit k, k multiple de 13, tel Fk=0 modulo k.

par **Doraki** » 23 Juil 2010, 19:15

J'crois bien que F_2184 = 0 mod 2184.

C'est marrant comme truc...
est-ce que pour tout n il existe un multiple n' de n tel que Fn' = 0 mod n' ?

par **nodjim** » 24 Juil 2010, 07:02

C'est une bonne réponse. En plus, en ne donnant que le résultat, tu ne dévoiles pas le secret pour l'obtenir, ça reste ouvert pour tous.
Sinon, si Fn=0 modulo n, alors, au moins, sauf erreur:
F5n=0 modulo 5n
Fn²=0 modulo n²
par exemple.

Reste à montrer, en généralisation, que tout nombre premier donné se retrouve dans la décomposition d'un "zéro Fibonacci".

par **Ben314** » 24 Juil 2010, 10:34

Bon, aprés avoir été un peu "sec" sur la façon de procéder, je pense avoir trouvé [par exemple le plus petit k multiple de 11 tel que k divise Fk est 660]

Mais, visiblement (comme Doraki), je ne comprend pas bien "pourquoi" ça marche (i.e. est-ce que la méthode marche quelque soit le nombre fixé au départ...).

Edit : je pense que oui...

par **Doraki** » 24 Juil 2010, 12:11

Pour n>=4, F(n!) est multiple de n!

par **nodjim** » 24 Juil 2010, 15:55

C'est assez normal, il me semble.
Pour compléter ma réponse à ta question, le produit de 2 "zéros Fibonacci" est également un "zéro Fibonacci".

par **nodjim** » 24 Juil 2010, 16:12

Ben314 a écrit:Bon, aprés avoir été un peu "sec" sur la façon de procéder, je pense avoir trouvé [par exemple le plus petit k multiple de 11 tel que k divise Fk est 660]

Mais, visiblement (comme Doraki), je ne comprend pas bien "pourquoi" ça marche (i.e. est-ce que la méthode marche quelque soit le nombre fixé au départ...).

Edit : je pense que oui...

Ok pour 660 avec 11.

par **Ben314** » 24 Juil 2010, 19:00

Bon, en fait, j'avais cru avoir une méthode, mais je suis un peu sec...

Comment évalue-t-on le plus petit entier n (pas forcément le mini, mais un pas trop grand...) tel que p² (ou p^3 ou...) divise n (avec p premier) ?

par **Doraki** » 24 Juil 2010, 19:38

Je note t(m) l'entier tel que Fn = 0 [m] <=> n = 0 [t(m)],

Si je me gourre pas,
t(p^k) = p^(k-1)*t(p), sauf pour p=2, où t(2^k) = 3,6,6,12,24,48...

Pour p=5, t(5) = 5
Pour p=3 ou 7 [10], t(p) divise (p+1)
Pour p=1 ou 9 [10], t(p) divise (p-1)

par **Ben314** » 25 Juil 2010, 00:03

Effectivement, je vient de voir que, pour tout p premier et tout n, on a

ce qui permet de montrer le résultat...

Edit : En fait, il me manque (encore) un dernier "détail" : pourquoi

n'est il pas divisible par

?

par **Doraki** » 25 Juil 2010, 10:32

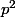Ben314 a écrit:En fait, il me manque (encore) un dernier "détail" : pourquoi n'est il pas divisible par ?

Ah oui tiens, j'ai oublié de me poser cette question.

par **Ben314** » 25 Juil 2010, 10:36

Ouf...
ça me rassure parce que, perso, j'ai "ramé" à presque toutes les étapes et d'ailleurs, j'ai toujours pas la solution à celle là d'étape... (est-ce vrai ?)

par **nodjim** » 25 Juil 2010, 18:20

Si vous arrivez à prouver que la somme des carrés de 2 nombres de Fibonacci successifs n'est pas le multiple d'un carré, alors je vous dirais pourquoi on ne peut abouter directement sur un p².

par **Ben314** » 25 Juil 2010, 21:54

nodjim a écrit:Si vous arrivez à prouver que la somme des carrés de 2 nombres de Fibonacci successifs n'est pas le multiple d'un carré, alors je vous dirais pourquoi on ne peut abouter directement sur un p².

Dans l'absolu, ce n'est pas tout à fait vrai :

est divisible par

, mais comme 5 joue un rôle trés particulier...
J'arrive à montrer que

ne peut pas être divisible par

ni par un

premier avec

mais je ne vois pas (pour le moment) pourquoi il ne serait pas divisible par un

où

(mais visiblement

)

par **Doraki** » 25 Juil 2010, 22:04

Ben par exemple, F7 = 13, et 13*7 = 91, donc F45² + F46² = F91 est un multiple de 13²
etc.

par **Ben314** » 25 Juil 2010, 22:13

Effectivement...
Donc je retourne a mes premières amours :

peut-il être divisible par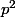

?

Remarque : en fait, pour montrer que, quelque soit m, il existe un multiple n de m tel que n divise Fn, on a pas besoin de ça : il suffit de savoir que

est divisible par

.
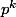Mais j'aimerais bien savoir quand même...

par **Doraki** » 25 Juil 2010, 22:22

J'ai testé jusqu'à p <= 32000 et ça marche, mais je sais pas pourquoi...

Et ça implique que si p = 3 mod 4, alors le premier Fn multiple de p apparaît pour n pair, si j'ai bien suivi ?

par **Ben314** » 25 Juil 2010, 22:34

Oui, mais en fait, c'est tout con :
Si

est divisible par un

, c'est à dire un irréductible de

alors

OU BIEN

est divisible par

ce qui entraine que

ET

sont divisible par p ce qui ne se peut vu qu'ils sont premiers entre eux.

par **Ben314** » 25 Juil 2010, 22:47

Par exemple, ça permet quand de dire que, si

et que

est premier alors le premier

multiple de

est

...

Les zéros Fibonacci

Les zéros Fibonacci

Qui est en ligne