Montrer que
Inégalité sympa
8 messages
- Page 1 sur 1
Re: Inégalité sympa
(avec égalité ssi
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité sympa
Ok 
 En poussant un peu plus loin vers les fonctions intégrables on arrive à :
En poussant un peu plus loin vers les fonctions intégrables on arrive à :
g(x)dx=0\Longrightarrow \frac {(\int_0^1f(x)dx)^2}{\int_0^1f^2(x)dx}+\frac{(\int_0^1g(x)dx)^2}{\int_0^1g^2(x)dx}\leq 1)
Do you agréé ?
Do you agréé ?

Modifié en dernier par MMu le 29 Avr 2024, 14:58, modifié 1 fois.
Re: Inégalité sympa
Il me semble bien que oui : en divisant f et g par leur norme (L_2) on retombe sur la même chose que précédemment avec L_2([0,1]) à la place de R^n.
Il faut juste mettre les bonnes hypothèses pour que tout existe (et que les dénominateurs soient non nuls).
En fait, en faisant la même chose (décomposer f et g suivant vec(h) et son orthogonal) on obtient la formule suivante (valable sans hypothèses dans tout préhilbertien) :
^2\|h\|^2\!+(g.h)^2\|f\|^2\!+(h.f)^2\|g\|^2\leqslant \|f\|^2\|g\|^2\|h\|^2+2(f.g)(g.h)(h.f))
(avec égalité ssi les trois vecteurs sont dans un même plan)
Et si on suppose , ça donne
, ça donne ^2}{\|f\|^2}+\dfrac{(g.h)^2}{\|g\|^2}\leqslant \|h\|^2)
Il faut juste mettre les bonnes hypothèses pour que tout existe (et que les dénominateurs soient non nuls).
En fait, en faisant la même chose (décomposer f et g suivant vec(h) et son orthogonal) on obtient la formule suivante (valable sans hypothèses dans tout préhilbertien) :
(avec égalité ssi les trois vecteurs sont dans un même plan)
Et si on suppose
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité sympa
En fait, si on suppose les trois vecteurs unitaires (ce qui ne change rien sur le principe), on a ça :
^2\!+(g.h)^2\!+(h.f)^2\leqslant 1+2(f.g)(g.h)(h.f))
Y-a-t-il une formule plus générale avec vecteurs telle que celle là corresponde au cas
vecteurs telle que celle là corresponde au cas 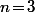 ?
?
Y-a-t-il une formule plus générale avec
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité sympa
La réponse est "oui" est c'est (archi)-connu.
Si tu as 3 vecteurs unitaires de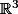 (*) et que tu pose
(*) et que tu pose  = la matrice 3x3 formée (en colonne) des coordonnées des 3 vecteurs (dans une b.o.n.) alors
= la matrice 3x3 formée (en colonne) des coordonnées des 3 vecteurs (dans une b.o.n.) alors  où
où  sont les produits scalaires des 3 vecteurs pris 2 à 2.
sont les produits scalaires des 3 vecteurs pris 2 à 2.
Et la matrice et non seulement symétrique, mais bien évidement elle est aussi positive donc son déterminant est positif ce qui donne précisément la formule du post précédent (et sans supposer les vecteurs unitaire, ben c'est la formule du post encore précédent).
et non seulement symétrique, mais bien évidement elle est aussi positive donc son déterminant est positif ce qui donne précisément la formule du post précédent (et sans supposer les vecteurs unitaire, ben c'est la formule du post encore précédent).
Et bien sur, ça se généralise avec un nombre quelconque de vecteurs et l'inégalité est une égalité ssi\!=\!0) c'est à dire ssi la famille de vecteurs est liée.
c'est à dire ssi la famille de vecteurs est liée.
(*) Et ça ne coûte rien de les supposer dans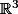 vu qu'à eux 3 ils engendrent un s.e.v. au max de dim. 3.
vu qu'à eux 3 ils engendrent un s.e.v. au max de dim. 3.
Si tu as 3 vecteurs unitaires de
Et la matrice
Et bien sur, ça se généralise avec un nombre quelconque de vecteurs et l'inégalité est une égalité ssi
(*) Et ça ne coûte rien de les supposer dans
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité sympa
Et ça permet de rédiger la solution de ton exercice de départ de façon plus directe :

 est }ns^2-(a^2\!+\!b^2)s\mbox{ donc }a^2\!+\!b^2\!\leqslant\!ns)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

