Mon idée initilale pour la démonstration n'était pas valable
À défaut d'avoir d'autre idée ...
Je la poste en trois parties
On montre que
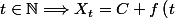\dfrac {1}{AC}\overrightarrow {CA})
Démonstration:
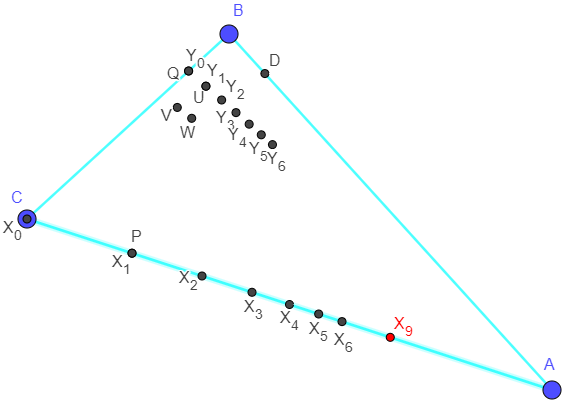
L'idée de cette démonstration là est en première partie de définir les points et les droites impliqué(e)s
dans la construction des points des deux familles
_{i\in \mathbb {N}})
et
_{i\in \mathbb {N}})
Puis dans un deuxième temps de définir une formulation générale des coordonnées barycentriques
des points des deux familles
_{i\in \mathbb {N}})
et
_{i\in \mathbb {N}})
à partir de
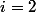
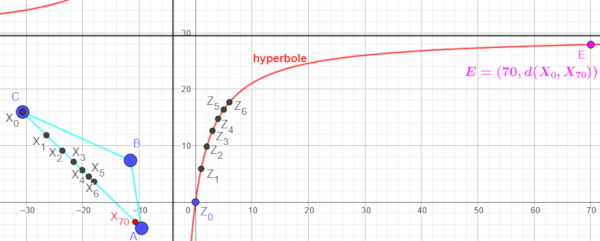
Puis dans un troisième temps à trouver la relation qui lie le point

à la valeur de
)
afin de conclure la démo
Première partie:1.Repère barycentrique et la constante

On considère un repère barycentrique
)
quelconque du plan
et on considère la constante réelle
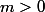
qui sera la somme des
coordonnées barycentriques d'un point quelconque du plan par rapport à
)
Cependant la somme des coordonnées barycentriques des droites ne sera pas toujours

2.Abréviation et vocabulaire
-Quand on dira que
)
sont les cb d'un point (resp. d'une droite)
on signifiera par là que
)
sont les coordonnées barycentriques de ce point (resp. de cette droite) par rapport au repère
)
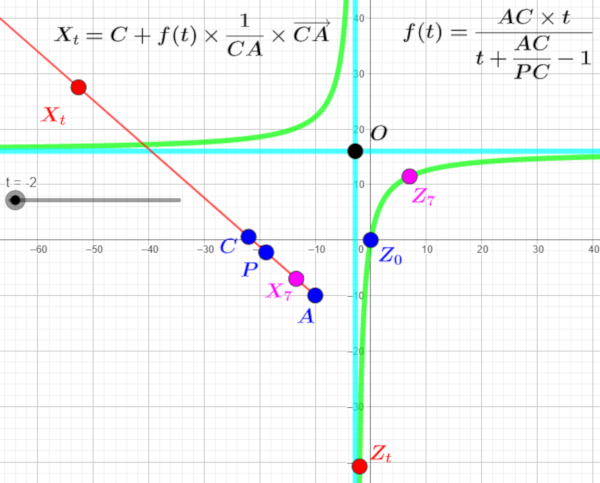
3.Les variables réelles

et

-Comme
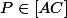
mais est distinct de

et de

à une variable réelle

dans l'intervalle
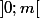
on va associer le point

dont les cb sont
)
De sorte qu'on vérifie
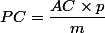
et
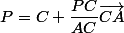
-Comme
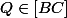
mais est distinct de

et de

à une variable réelle

dans l'intervalle
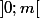
on va associer le point

dont les cb sont
)
De sorte qu'on vérifie
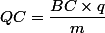
et
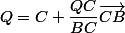
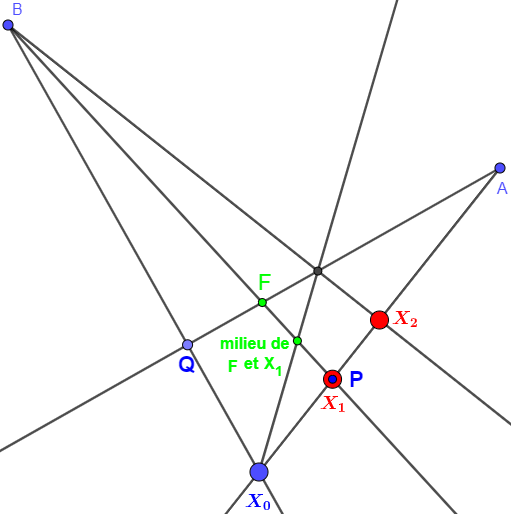
4.Points et droites à établir au préalable
)
sont les cb de

et de
)
)
sont les cb de

et de
)
)
sont les cb de

et de
)
)
sont les cb de

)
sont les cb de

)
sont les cb de
)
)
sont les cb de
)
)
sont les cb de
)
)
sont les cb de

selon
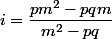
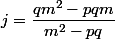
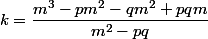
)
sont les cb de
)
selon:
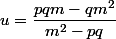
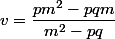
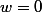
)
sont les cb de

selon:
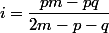
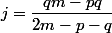
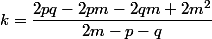
)
sont les cb de
)
selon:
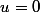
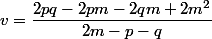
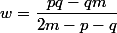
)
sont les cb de
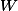
selon:
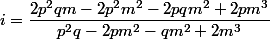
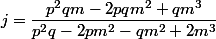
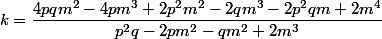
)
sont les cb de
)
selon:
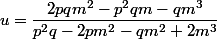
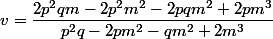
)
sont les cb de

selon:
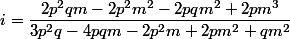
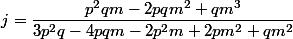
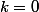
la deuxième partie viendra quand j'aurais le temps