Hyperbole par Ptolémée

[azf]

Bonjour

Je propose ce problème que je trouve beau car il est de solution très simple dans sa construction

Les données:
Dans le plan
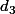
Un point et trois droites distinctes deux à deux , , tels que
Les droites et sont sécantes
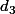
La droite rencontre les deux droites et en deux points distincts
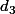
La droite passe par le point
Les deux droites et ne passent pas par le point
n'appartient pas au triangle engendré par les trois droites
Le problème:
À la règle non graduée et au compas construire quatre points tels que
d'une part et sont les deux asymptotes de l'hyperbole passant par
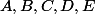
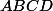
et d'autre part est un quadrilatère convexe inscriptible

[azf]

On devinera facilement la construction à faire avec cette figure qui dit tout

[azf]

Je n'avais pas prévu ça mais je n'ai pas le temps donc du coup je poste la solution tout de suite car je dois partir faire autre chose

Solution:
intersection de et
intersection de et
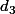
intersection de et
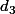
le milieu de
le symétrique de par rapport à
le symétrique de par rapport à
le symétrique de par rapport à
la médiatrice de
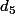
la médiatrice de
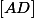
l'intersection de et
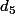
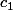
le cercle de centre passant par
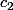
le cercle de centre passant par
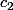
Le point tel que et sont l'intersection du cercle et de la droite
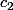
Le point tel que et sont l'intersection du cercle et de la droite
la droite passant par et
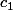
Le point tel que et sont l'intersection du cercle et de la droite
Fin.

[azf]

L'énoncé n'est pas correct : il manque de dire

n'appartient pas au triangle engendré par les trois droites

bon j'édite l'énoncé ainsi corrigé

[azf]

De toute façon le mieux est que je revienne démontrer ça car je ne suis pas certain qu'il y a des cas particuliers qui font que ma construction ainsi donnée donne toujours ce qui est attendu

La démo se basera sur la conique engendrée par ABCDE ainsi construite
-définir son équation cartésienne
-réduire cette équation
-démontrer que son excentricité est supérieure à 1
-définir les deux asymptotes et enfin démontrer que ce sont bien les deux droites et

Bon bah je reviendrai ...

[azf]

par déplacement et s'éviter la réduction, la démo pourra se simplifier en posant

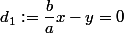
et

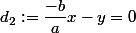
et après poser A qui devra vérifier les assertions de l'énoncé

ça va la simplifier pas mal même si elle sera moche quand même