Exo sympa
Olympiades mathématiques, énigmes et défis
-
ramanujo
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Aoû 2006, 16:38
-
 par ramanujo » 17 Aoû 2006, 20:58
par ramanujo » 17 Aoû 2006, 20:58
Soit

une bijection de

dans

.
Prouver que l'on peut trouver trois entiers

et

verifiant:
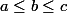
et
 + f(c)= 2 f(b))
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Aoû 2006, 00:02
par aviateurpilot » 18 Aoû 2006, 00:02
:ptdr:
si on prend
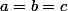
, alors
+f(c)=2f(b))
je penses que tu voulais dire
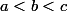
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Aoû 2006, 00:24
par aviateurpilot » 18 Aoû 2006, 00:24
soit a de IN
parmi les antécédants de
+1,f(a)+2,...,f(a)+a+1)
,il existe un dont l'image est
)
car il n'y a que

nombres
)
(*)[/quote]il existe surement un anticédent de
-f(a))
(car f est bijectif)
soit

ce antécédant.
dans ce cas
=2f(b)-f(a))
+f(c)=2f(b))
.
et
=f(b)+(f(b)-f(a))>f(b)>f(a))
, donc
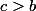
d'apres (*)
ce que j'ai montrer jusqu'à present c'est:
quelque soit a de IN, ils existent c et b tel que,
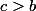
et
+f(c)=2f(b))
il ne me rest alors que prendre un

inferieure strictement à

sans se cassé la tete :marteau: en prend a=0
:zen:
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 18 Aoû 2006, 00:29
par El_Gato » 18 Aoû 2006, 00:29
Définissons
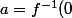)
et soit

l'ensemble:
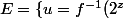, u > a \; \mbox{et} \; z \geq 1 \})
. E est non vide (car f est bijective), et minoré par a. Soit b = Min E, avec
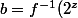)
pour un unique z. On a
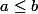
par définition du min. Soit
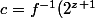)
. On a

et
 + f(c) = 2^{z+1}= 2 \times 2^z = 2f(b))
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Aoû 2006, 00:38
par aviateurpilot » 18 Aoû 2006, 00:38
on a
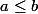
par définition du min
mais

n'appartient pas à E
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 18 Aoû 2006, 00:40
par El_Gato » 18 Aoû 2006, 00:40
aviateurpilot a écrit:mais

n'appartient pas à E
Non, et alors ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Aoû 2006, 00:45
par aviateurpilot » 18 Aoû 2006, 00:45
dsl, j'ai pas bien lu ta solution
c clair mtn :++:
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 18 Aoû 2006, 00:51
par El_Gato » 18 Aoû 2006, 00:51
aviateurpilot a écrit:dsl, j'ai pas bien lu ta solution
c clair mtn :++:
Ciao a plus. Il est deux heures du mat j'y vais.
-
ramanujo
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Aoû 2006, 16:38
-
 par ramanujo » 18 Aoû 2006, 15:09
par ramanujo » 18 Aoû 2006, 15:09
je penses que tu voulais dire a<b<c
Ouais c'est ca..j'avais oublié.
Sinon j'avais fait le même raisonnement que aviateurpilot en prenant l'ensemble
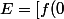<f(n); n\in N])
..et avec

.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 19 Aoû 2006, 20:58
par nekros » 19 Aoû 2006, 20:58
Salut,
On considère l'ensemble
 \le g(\alpha) })
avec
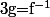
et
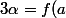)
et

.
L'ensemble est une partie finie : il existe donc

tel que :

,
 > g(\alpha))
On considère la suite
)
qui ne peut être strictement décroissante.
Donc il existe

tel que :
 \ge g(\alpha +2^{n}k))
Or,

et comme g est bijective, on a :
 > g(\alpha +2^{n}k))
On note
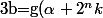)
et
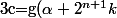)
.
On a donc

et :
=2(\alpha +2^{n}k)=\alpha + (\alpha +2^{n+1}k)=f(a)+f(c))
A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
+1,f(a)+2,...,f(a)+a+1) ,il existe un dont l'image est
,il existe un dont l'image est ) car il n'y a que
car il n'y a que  nombres
nombres ) (*)[/quote]il existe surement un anticédent de
(*)[/quote]il existe surement un anticédent de -f(a)) (car f est bijectif)
(car f est bijectif) ce antécédant.
ce antécédant.=2f(b)-f(a))
+f(c)=2f(b)) .
.=f(b)+(f(b)-f(a))>f(b)>f(a)) , donc
, donc 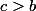 d'apres (*)
d'apres (*)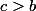 et
et +f(c)=2f(b))
 inferieure strictement à
inferieure strictement à 
