Existence d'une suite

[aviateur]

Bonjour
Existe-t-il une suite de réels telle que chaque polynôme
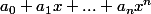admette exactement n racines réelles?

[nodgim]

Si tu écris le polynôme sous la forme :
(x-a1)(x-a2)(x-a3)..... ?

[aviateur]

Bonjour
@Nogdim, pourquoi pas, mais ton idée ne répond pas à la question car chaque polynôme de degré n que tu proposes(nommons le p_n) ne mène pas à la solution car à chaque fois les coordonnées dans la base canonique change. Pour être plus clair il suffit de voir que le terme constant de chaque p_n est le même et ce n'est pas le cas pour toi.

[nodgim]

Juste. C'est plus compliqué.

[Ben314]

Salut,
La réponse est oui et il y a deux preuves (essentiellement différentes) possibles :

(1) Théorique, plus général et très facile : on montre qu'étant donné un polynôme quelconque de degré ayant racine le polynôme aura 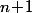racines pour toute valeur (non nulle) de suffisamment proche de zéro.

(2) Plus compliqué (et moins général) On donne une suite explicite de et on montre qu'avec cette suite là, ça marche (j'ai pas d'exemple en tête avec une preuve simple)

[nodgim]

C'est vrai que sur plan ça marche bien: on ajoute un polynôme an*x^n avec un faible "an" pour garder les racines existantes à peu près à l'endroit où elles sont, la racine supplémentaire venant d'elle même.

[aviateur]

Bonjour
Tout à fait d'accord avec ta réponse 1 @ben.
Pour la 2. je ne trouve pas d'exemple explicite.
Comme il y a des solutions, pour l'une quelconque d'entre elles, on peut poser et supposer que le rayon de convergence est infini.
Puis éventuellement trouver un bon candidat f(x) ...?