Montrer que dans tout intervalle
Existence
2 messages
- Page 1 sur 1
Existence
Soient les fonctions 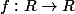 (réels) et
(réels) et 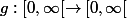 telle que
telle que >0)
Montrer que dans tout intervalle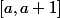 il existe
il existe 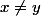 tels que
tels que
+f(y)}2<f(\frac{x+y}2)+g(|x-y|))
Montrer que dans tout intervalle
Re: Existence
Salut,
Soit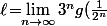\,>\,0) . Il existe donc
. Il existe donc  tel que
tel que \!\geq\!\frac{\ell}{2\times 3^n}) .
.
On suppose par l'absurde que pour tout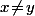 de
de 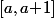 on a
on a +f(y)}2\geq f(\frac{x+y}2)\!+\!g(|x-y|)) .
.
En particulier, pour tout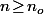 et
et 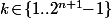 , si on prend
, si on prend 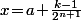 et
et 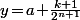 on obtient que
on obtient que
\!-\!2f(a\!+\!\frac{k}{2^{n+1}})\!+\!f(a\!+\!\frac{k+1}{2^{n+1}})\geq 2g(\frac 1{2^n})\geq\frac{\ell}{3^n}\ \ (I_k))
\!\!\times\!\!I_{2^n+1}\!+\!(2^n\!\!-2)\!\!\times\!\!I_{2^n+2}\!+\!...\!+\!1\!\!\times\!\!I_{2^{n+1}-1}) donne alors
donne alors
\!-\!2f(a\!+\!\frac{1}{2})\!+\!f(a\!+\!1)\geq2^{2n}\!\times\!\frac{\ell}{3^n})
Ce qui est absurde vu que le terme de gauche est constant et que celui de droite tend vers +oo.
Soit
On suppose par l'absurde que pour tout
En particulier, pour tout
Ce qui est absurde vu que le terme de gauche est constant et que celui de droite tend vers +oo.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
