Salut,
En fait, c'est un simple (mais gros) système linéaire à résoudre : si on note

les valeurs inscrites sur les 12 sommets on a 12 équations linéaires
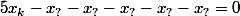
où les 5 ? désignent les numéros des sommets adjacents au sommet

.
Après, modulo que je ne me sois pas gourré dans la saisie de la matrice, le polynôme caractéristique de cette dernière est
=\lambda(\lambda\! +\! 6)^5(\lambda^2\!+\!10\lambda\!+\!20)^3)
donc le noyau n'est que de dimension 1 et bien évidement, engendré par le vecteur (1,1,...,1) donc les seules solutions sont celles où les valeurs sur les sommets sont toutes les mêmes.
EDIT : j'ai mal lu l'énoncé et j'ai fait comme si TOUTES les valeurs des sommets étaient la moyennes des voisins alors que ce n'est pas forcément le cas pour les deux sommets de départ. Mais bon, c'est quand même juste un système linéaire à résoudre . . .
P.S. Après calculs, je trouve 2024+1012+736+736+1012

