Exercice duficile
Olympiades mathématiques, énigmes et défis
-
haking007
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Déc 2009, 21:02
-
 par haking007 » 30 Déc 2009, 20:28
par haking007 » 30 Déc 2009, 20:28
qui peux me résoudre cet exercice :mur:

:marteau: :
Montrer que pour n entier, il existe un entier m tel que :

-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Déc 2009, 20:31
par lapras » 30 Déc 2009, 20:31
Bonjour, C'est un devoir ou un exo d'olympiade ?
-
sniperamine
- Membre Relatif
- Messages: 366
- Enregistré le: 19 Jan 2009, 03:46
-
 par sniperamine » 30 Déc 2009, 21:04
par sniperamine » 30 Déc 2009, 21:04
exercice focile !!
-
haking007
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Déc 2009, 21:02
-
 par haking007 » 30 Déc 2009, 21:05
par haking007 » 30 Déc 2009, 21:05
oui; je sais mais je veux le reponse
-
Anonyme
 par Anonyme » 31 Déc 2009, 11:44
par Anonyme » 31 Déc 2009, 11:44
Je suis aussi intéressé par la résolution de cet exo.
Est ce que quelqu'un peut donner une indication ?
J'ai essaye par récurrence mais cela n'a pas marche ..
-
haking007
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Déc 2009, 21:02
-
 par haking007 » 31 Déc 2009, 12:33
par haking007 » 31 Déc 2009, 12:33
non il n y pas d'indication ; moi j'écris l'exercice tel qu-il est
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 31 Déc 2009, 13:07
par lapras » 31 Déc 2009, 13:07
Bon pour Qmath : montre effectivement par récurrence que
^n = a_n + b_n\sqrt{2})
et que

En fait ca se voit avec le conjugué de la puissance qui est la puissance du conjugué et on a
(sqrt{2}+1)=1)
.
-
Anonyme
 par Anonyme » 31 Déc 2009, 13:37
par Anonyme » 31 Déc 2009, 13:37
Merci beaucoup lapras. :zen:
Quand on demontre ces deux realtion le probleme est presque resolu et il ne reste que de conclure.
J'ai juste une question concernant les conjugues:
Est ce que si on a

peut on dire toujours que leur conjugue sont egaux ?
Si oui pourquoi ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Déc 2009, 13:43
par Doraki » 31 Déc 2009, 13:43
Tu te demandes si le produit des conjugués est le conjugué du produit ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 31 Déc 2009, 13:46
par lapras » 31 Déc 2009, 13:46
Salut en fait c'est un peu comme dans les complexes le produit du conjugué c'est le conjugué du produit.
-
Anonyme
 par Anonyme » 31 Déc 2009, 13:54
par Anonyme » 31 Déc 2009, 13:54
J'ai pas encore fais les complexes donc j'attendrais ..
Merci pour tout
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 31 Déc 2009, 14:04
par lapras » 31 Déc 2009, 14:04
Enfin tu peux quand même vérifier que le conjugué du produit est le produit du conjugué, où le conjugué de x=a+bsqrt(2) est a-bsqrt(2).
-
Anonyme
 par Anonyme » 31 Déc 2009, 14:11
par Anonyme » 31 Déc 2009, 14:11
En effet.
Lapras ca te dérange tu je t'envoie ma demo par mp (des que je l'aurai faite) pour la corriger ?
J'aimerais pas la poster sur le forum et faire son devoir a sa place.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 31 Déc 2009, 15:11
par lapras » 31 Déc 2009, 15:11
Ok je vais voir ca.
-
haking007
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Déc 2009, 21:02
-
 par haking007 » 31 Déc 2009, 22:39
par haking007 » 31 Déc 2009, 22:39
c'est bient de duscuter mais je n'ai pas trouver aucun demostration idèeale
mais pour "lapras" je voudrez inducer votre methode SVP
en fin merci a tous
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 01 Jan 2010, 16:03
par kasmath » 01 Jan 2010, 16:03
c'est un exo d'olympiades international
-
Anonyme
 par Anonyme » 01 Jan 2010, 16:35
par Anonyme » 01 Jan 2010, 16:35
quels sont tes sources ?
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 02 Jan 2010, 14:40
par kasmath » 02 Jan 2010, 14:40
Qmath a écrit:quels sont tes sources ?
ok quand je vais le trouver je vais te le dire
-
haking007
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Déc 2009, 21:02
-
 par haking007 » 02 Jan 2010, 17:35
par haking007 » 02 Jan 2010, 17:35
moi je trouve la solution :ptdr: :id:
reponse:
1_) on pose sqrt(x)=s(x).
2_) on sait que s(m)-s(m-1)=(s(2)-1)^n......(1)
d'autre part (s(m)-s(m-1))(s(m)+s(m-1))/(s(m)+s(m-1))=(s(2)-1)^n
impq : 1/(s(m)+s(m-1))=(s(2)-1)^n
impq : s(m)+s(m-1)=1/(s(2)-1)^n=(s(2)+1)^n .......(2)
alors on a :
(1)....s(m)-s(m-1)=(s(2)-1)^n
(2)....s(m)+s(m-1)=(s(2)+1)^n
donc (1).+(2). est :
2s(m)=(s(2)-1)^n+(s(2)+1)^n
on pose :(s(2)-1)^n+(s(2)+1)^n=X
alors s(m)=1/2(X)
impq m=1/4(X^2) :we: :zen:
votre frere haking007
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 02 Jan 2010, 19:31
par benekire2 » 02 Jan 2010, 19:31
on sait que
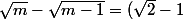^n)
(1)
d'autre part
(\sqrt{m}+\sqrt{m-1})}{\sqrt{m}+\sqrt{m-1}}=(\sqrt{2}-1)^n)
implique :
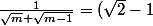^n)
implique :
^n}=(\sqrt{2}+1)^n)
(2)
alors on a :
(1)....
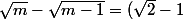^n)
(2)....
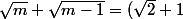^n)
donc (1)+(2) donne :
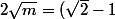^n+(\sqrt{2}+1)^n)
on pose :
^n+(\sqrt{2}+1)^n=X)
alors
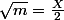
implique
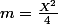 Voilà écrit en TEX
Voilà écrit en TEX
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités

