Trouver toutes les f solutions.
Equations fonctionnelles
18 messages
- Page 1 sur 1
Ah une equation fonctionnelle,ca faisait longtemps lol.Bon ben premier arrivé,premier servi.
-En prenant y=0,on a fof(x)=f(x²),donc si f est injective,f(x)=x²
-Si f n est pas injective,il existe a,b distincts tels que f(a)=f(b).En prenant x=a puis x=b,on obtient f(a²-y)=f(b²-y) donc f est periodique de periode T=b²-a²
-En prenant y=0 puis y=T on obtient 4Tf(x)=0 donc f=0
C est pas la plus dure que t aies donnée.
-En prenant y=0,on a fof(x)=f(x²),donc si f est injective,f(x)=x²
-Si f n est pas injective,il existe a,b distincts tels que f(a)=f(b).En prenant x=a puis x=b,on obtient f(a²-y)=f(b²-y) donc f est periodique de periode T=b²-a²
-En prenant y=0 puis y=T on obtient 4Tf(x)=0 donc f=0
C est pas la plus dure que t aies donnée.
Ok ca marche
on pouvait aussi remarquer facilement en prenant y = x² puis y = -f(x) que f(x)=x² ou f(x) = 0
en supposant qu'il existe a / f(a) = 0
on montre que alors f(x) = 0 pour tout x (pour cela on prend x = a, f(y) = f(a²-y), or si y != a²/2, y² != (a²-y)² donc f(y) = 0, le cas y = a²/2 est facile aprouver que f(a²/2) = 0)
donc f(x) = x² pour tou x ou f(x) = 0 pour tout x :++:
C'est vrai qu'elle était simple,
mais t'inquiete pas je vais relancer la mode ca va être marran ! :we:
on pouvait aussi remarquer facilement en prenant y = x² puis y = -f(x) que f(x)=x² ou f(x) = 0
en supposant qu'il existe a / f(a) = 0
on montre que alors f(x) = 0 pour tout x (pour cela on prend x = a, f(y) = f(a²-y), or si y != a²/2, y² != (a²-y)² donc f(y) = 0, le cas y = a²/2 est facile aprouver que f(a²/2) = 0)
donc f(x) = x² pour tou x ou f(x) = 0 pour tout x :++:
C'est vrai qu'elle était simple,
mais t'inquiete pas je vais relancer la mode ca va être marran ! :we:
grace a (3),on peut etendre f sur R+² en gardant les 3 propriéts,en posant par exemple f(0,y)=f(1,1+y)-1.(on pourrait meme etendre f sur R² en fait).Ensuite,si on pose a=f(1,0),on a pour x>y:
f(x,y)=f(x-y,0)+y=(x-y)a+y=ax+(1-a)y.
Si x
La positivité de f entraine a dans [0,1],et ces fonctions verifient bien 1,2 et 3 donc la reponse est:l enveloppe convexe de {max,min}
f(x,y)=f(x-y,0)+y=(x-y)a+y=ax+(1-a)y.
Si x
La positivité de f entraine a dans [0,1],et ces fonctions verifient bien 1,2 et 3 donc la reponse est:l enveloppe convexe de {max,min}
ayé:
-y=0 donne f(x²)=(x-1)f(x).En particulier on a f(0)=0,f(1)=0,et f(x) est nul si et seulement si f(x²) est nul.si et seulement si f(-x)=0.il suffit donc de montrer que f est nulle sur R+*
-y=1-x donne 2f(x²-x+1)=f(1)=0 donc f est nulle sur l image de x²-x+1,a savoir sur [1/4,+infini[.si a est strictement compris entre 0 et 1/4.en prenant plusieurs fois la racine carrée de a,on finira par tomber sur un reel strictement plus grand que 1/4,donc en utilisant f(x)=0 si et seulement si f(x²)=0,on en deduit f(a)=0
-y=0 donne f(x²)=(x-1)f(x).En particulier on a f(0)=0,f(1)=0,et f(x) est nul si et seulement si f(x²) est nul.si et seulement si f(-x)=0.il suffit donc de montrer que f est nulle sur R+*
-y=1-x donne 2f(x²-x+1)=f(1)=0 donc f est nulle sur l image de x²-x+1,a savoir sur [1/4,+infini[.si a est strictement compris entre 0 et 1/4.en prenant plusieurs fois la racine carrée de a,on finira par tomber sur un reel strictement plus grand que 1/4,donc en utilisant f(x)=0 si et seulement si f(x²)=0,on en deduit f(a)=0
Okay ca marche.
Moi je l'ai résolue de cette maniere mais aussi d'une autre en admettant que f est continue en 0,
On voit facilement que = f(0) = 0) (1)
(1) 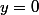 =>
=> = (x - 1)f(x))
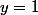 =>
=>  = f(x + 1) = f((x + 1))^2)
or^2 + 1) = f((1 - x)^2) = f(x^2 + 1) = f((1 + x)^2))
=>
(2) = f(x^2 - 2x + 1) = f(x^2))
Supposons que tel que
tel que  \neq 0)
par (1) : = 0 f(a) = 0) (car
(car 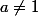 )
)
if
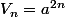 est décroissante et puisque
est décroissante et puisque  est continue en 0.
est continue en 0.
 \neq 0) absurde
absurde
donc = 0 \forall x \in \mathbb{R})
Si
Soit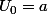
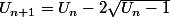
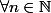 on a
on a  = 0) :
:
Il est facile de voir que est décroissante jusqu'a
est décroissante jusqu'a  tel que
tel que  = 0 \forall x \in \mathbb{R})
Si on prend
on prend 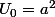 et
et  = 0)
( )
)
donc
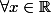
 = 0)
Moi je l'ai résolue de cette maniere mais aussi d'une autre en admettant que f est continue en 0,
On voit facilement que
or
=>
(2)
Supposons que
par (1) :
if
donc
Si
Soit
Il est facile de voir que
Si
(
donc
rafbh a écrit:Ou est ce qu'on trouve ces cours?
Merci!
Excuse moi je n'avais pas vu ton post !
Voilà le lien : http://www.animath.fr/tutorat.html#Les%20cours%20de%20l%27Olympiade%20fran%C3%A7aise%20de%20math%C3%A9matiques
Lis bien, tu comprendras mieux après
rafbh a écrit:Comment peut on savoir qu'il n'existe que ces deux solutions??
Vous navez traité que pour y=0!
Ca peut sembler bete mais bon!
Merci :mur:
Tu as presque raison,ya un petit truc qu on ne dit pas:Ce qu on dit,c est que si une fonction qui verifie la relation,alors elle doit la vérifier en particulier pour y=0 par exemple,puis en bidouillant on obtient que on doit avoir f(x)=x² ou f(x)=0.On obtient donc que si une fonction verifie la relation,alors c est l une de ces 2 fonctions.Mais ce qu il faut verifier ensuite,c est la reciproque:est-ce que ces fonctions verifient la relation pour tout x et tout y.Et ca on le laisse generalement au lecteur car c est juste un petit calcul de verification
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
