Equations fonctionnelles
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 20 Juil 2006, 00:57
par nekros » 20 Juil 2006, 00:57
Bonsoir,
Soit
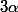
et
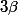
dans
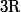
.
Trouver toutes les fonctions

de

dans
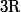
telles que pour tout

et


:
f(y)=y^{\alpha}f(\frac{x}{2})+x^{\beta}f(\frac{y}{2})})
Bonne chance.
Thomas G :zen:
-
buzard
- Membre Relatif
- Messages: 274
- Enregistré le: 22 Mai 2006, 14:29
-
 par buzard » 20 Juil 2006, 12:59
par buzard » 20 Juil 2006, 12:59
Pas mal l'equation,
j'obtiens comme solutions (suivant les valeurs de alpha et beta)
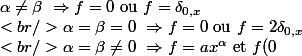=0)
avec

et a un réel positif ou nul.
si on impose la continuité à droite en 0, alors il ne reste plus que

avec
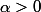
J'ai essayer de montrer que f etait dérivable à droite en 0 (pour obtenir la continuité) mais j'y suis pas arrivé, si quelqu'un à une idée ca m'interesse.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 22 Juil 2006, 00:33
par nekros » 22 Juil 2006, 00:33
Buzard, peux-tu détailler ton raisonnement ?
Il faut voir que comme

et
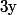
jouent des rôles symétriques dans le membre de gauche, il doit en être de même dans le membre de droite.
On a donc pour

et

:
+x^{\beta}f(\frac{y}{2})=x^{\alpha}f(\frac{y}{2})+y^{\alpha}f(\frac{x}{2}))
Il reste à traiter les cas

et

Thomas G :zen:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 22 Juil 2006, 01:40
par aviateurpilot » 22 Juil 2006, 01:40
a=alpha et b=beta
on a
+x^bf(y/2)=f(x)f(y))
(1)
et
f(x)=x^af(y/2)+y^bf(x/2))
(y^a-y^b)=f(y/2)(x^a-x^b))
(*)
si on prend y=1 dans la relation (*) on trouve que f(1/2)=0.
et on a d'apre (1) :
^2=2f(1/2)=0)
donc f(1)=0
en replacant y par 2 dans (*) on trouve :
quelque soit x de R
(2^a-2^b)=0) si
si 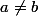 alors f est une fonction constante
alors f est une fonction constante =0)
et il rest le cas ou a=b
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 22 Juil 2006, 01:42
par aviateurpilot » 22 Juil 2006, 01:42
nekros a écrit:faut voir que comme x et y jouent des rôles symétriques dans ...............
quandtu as posté ca
j'ete entraine d'ecrire ma solution :++:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Juil 2006, 00:26
par nekros » 23 Juil 2006, 00:26
La réponse de aviateurpilot est correcte pour le cas \alpha \neq \beta.
Pour

, on a :
Pour

avec

et

, on remarque que
=\frac{1}{2}\frac{1}{x^{\alpha}}(f(x))^2)
On a donc
f(y)=\frac{1}{2}y^{\alpha}\frac{1}{x^{\alpha}}(f(x))^2+\frac{1}{2}x^{\alpha}\frac{1}{y^{\alpha}}(f(y))^2)
On a donc
}{x^{\alpha}}=\frac{f(y)}{y^{\alpha}})
Donc
}{x^{\alpha}}=c)
avec

pour

Donc
=cx^{\alpha})
L'équation initiale s'écrit donc :
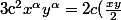^{\alpha})
On trouve facilement que

ou

Les solutions sont donc

et

Reste à vérifier la réciproque.
Thomas G :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités