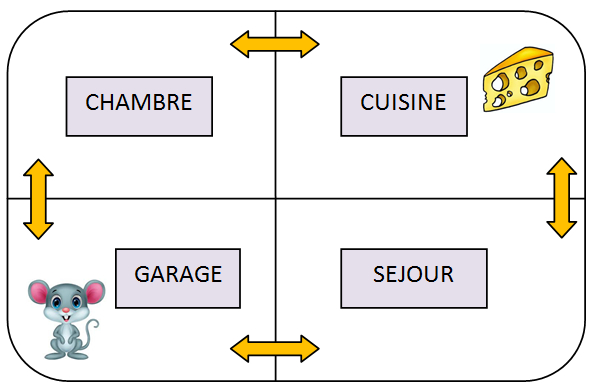
Une maison de campagne comporte 4 pièces : une cuisine, un séjour, une chambre et un garage.
A l’instant t = 0, une souris se trouve dans le garage. Elle peut aller et venir dans chaque pièce en passant par les trous symbolisés par les flèches jaunes.
Toutes les minutes, il y a :
– 50 % de chance que la souris reste dans la pièce où elle est actuellement ;
– 25 % de chance que la souris passe dans une pièce voisine.
Par exemple, pour t = 1 minute, la probabilité que la souris reste dans le garage est égale à 0,50, la probabilité que la souris passe dans la chambre est égale à 0,25 et enfin la probabilité qu’elle passe dans le séjour est égale à 0,25.
Important : Dès que la souris a atteint la cuisine (donc le fromage) elle ne repart plus dans les autres pièces. Elle mange tranquillement le fromage.
Il s’agit de répondre aux deux questions suivantes :
Question Q1 :
Déterminer le nombre de minutes tel que la probabilité que la souris atteigne le fromage soit supérieure à 99 %
Question Q2 :
Quel est le temps moyen (nombre moyen de minutes) mis par la souris pour atteindre le fromage ?

