Soit les formules suivantes :
B / A = C²
√109601 / C = A
√109601 * C = B
109601 / C = √109601 * A
109601 / B = √109601 / C
109601 / C² = A²
En réduisant la redondance entre les formules et en utilisant les correspondances entre ces six formules, pouvez-vous calculer les valeurs de A, B et C ?
Je précise que l'on recherche des solutions non nulles et non égales à un ou à moins un.
Je précise également que A et B sont des nombres entiers non égaux.
Je précise enfin que le problème n'admet qu'une seule et unique solution respectant ces conditions.
Ce qui m'intéresse ici n'est pas seulement que vous arriviez à trouver les valeurs, mais que vous puissiez justifier d'un raisonnement mathématique conduisant aux valeurs à partir de ces formules.
Enigme mathématique - Equation à résoudre
10 messages
- Page 1 sur 1
Enigme mathématique - Equation à résoudre
Modifié en dernier par coinroad le 22 Déc 2020, 15:56, modifié 3 fois.
Re: Enigme mathématique - Equation à résoudre
Bonjour,
La seconde ligne donne AC=331,06
La quatrième ligne donne AC=109601/331,06
Il n'y a donc pas de solution car 331,06 n'est pas égal à 109601 / 331,06.
Il est donc nécessaire de considérer ici que ce n'est pas 331,06, mais la racine carrée de 109601 (qui fait presque 331,06).
Alors les lignes 2 et 3 sont équivalentes ensembles à la première puisque si on divise la troisième par la seconde, on obtient la première.
La quatrième ligne est alors une conséquence de la seconde en divisant par la racine de 109601, et la dernière ligne n'est autre que la troisième élevée au carré.
On peut donc conserver les trois équations suivantes
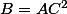
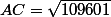
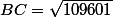
Les deux dernières donnent A=B et la première donne alors C=1 puis A=B= racine carrée de 109601 (soit à peu près 331,06)
PS. J'ai oublié de préciser au départ : on cherche des solutions non nulles puisque l'on divise par A, par B et par C. Ca tombe bien car la solution trouvée ne comporte aucun membre nul.
La seconde ligne donne AC=331,06
La quatrième ligne donne AC=109601/331,06
Il n'y a donc pas de solution car 331,06 n'est pas égal à 109601 / 331,06.
Il est donc nécessaire de considérer ici que ce n'est pas 331,06, mais la racine carrée de 109601 (qui fait presque 331,06).
Alors les lignes 2 et 3 sont équivalentes ensembles à la première puisque si on divise la troisième par la seconde, on obtient la première.
La quatrième ligne est alors une conséquence de la seconde en divisant par la racine de 109601, et la dernière ligne n'est autre que la troisième élevée au carré.
On peut donc conserver les trois équations suivantes
Les deux dernières donnent A=B et la première donne alors C=1 puis A=B= racine carrée de 109601 (soit à peu près 331,06)
PS. J'ai oublié de préciser au départ : on cherche des solutions non nulles puisque l'on divise par A, par B et par C. Ca tombe bien car la solution trouvée ne comporte aucun membre nul.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Enigme mathématique - Equation à résoudre
Bonjour, votre remarque est tout à fait juste concernant la valeur 331,06 que j'ai remplacé par √109601 afin de simplifier la présentation et éviter les erreurs de calcul liées à l'inexactitude de 331,06.
Par contre le résultat que vous donnez pour A , B et C n'est pas juste. En effet vous voyez dans les formules que si 109601 / B = √109601 / C et si √109601 / C = A alors cela signifie donc nécessairement par transitivité que 109601 / B = A.
Attention ce problème n'est pas aussi simple qu'il en a l'air ! L'objectif ici étant de savoir si l'on peut calculer la valeur de A, B, C en utilisant seulement les formules qui ont été communiquées.
Par contre le résultat que vous donnez pour A , B et C n'est pas juste. En effet vous voyez dans les formules que si 109601 / B = √109601 / C et si √109601 / C = A alors cela signifie donc nécessairement par transitivité que 109601 / B = A.
Attention ce problème n'est pas aussi simple qu'il en a l'air ! L'objectif ici étant de savoir si l'on peut calculer la valeur de A, B, C en utilisant seulement les formules qui ont été communiquées.
Re: Enigme mathématique - Equation à résoudre
Bonjour,
La solution que j'ai donné fonctionne, j'ai juste oublié le cas : C^2=1 donc C=1 ou C=-1. Il y a donc deux solutions qui sont d'une part celle que j'ai donné, d'autre part leurs opposées.
En particulier, au regard de votre remarque, 109601/B, c'est 109601 divisé par la racine carrée de 109601, et cela fait très exactement la racine carrée de 109601... Donc A (dans le cas de la solution "positive", mais elle fonctionne aussi avec la solution "négative").
On peut vérifier d'ailleurs : pour simplifier, j'appelle N le nombre 109601 et R la racine carrée de N.
Si A=B=R et C=1 on a alors en se souvenant que N=R*R
B / A = C² oui car R/R=1
√109601 / C = A oui car R/1=R
√109601 * C = B oui car R*1=R
109601 / C = √109601 * A oui car N/1=R*R
109601 / B = √109601 / C oui car N/R=R/1
109601 / C² = A² oui car N/1=R*R
Les résultats sont identiques si on remplace A et B par -R, et C par -1.
Le résultat est généralisable à tout N>0 et R racine carrée de N.
Enfin, si on ne cherche que des solutions différentes de 1, seule la solution C=-1 est correcte (donc A=B=-R).
La solution que j'ai donné fonctionne, j'ai juste oublié le cas : C^2=1 donc C=1 ou C=-1. Il y a donc deux solutions qui sont d'une part celle que j'ai donné, d'autre part leurs opposées.
En particulier, au regard de votre remarque, 109601/B, c'est 109601 divisé par la racine carrée de 109601, et cela fait très exactement la racine carrée de 109601... Donc A (dans le cas de la solution "positive", mais elle fonctionne aussi avec la solution "négative").
On peut vérifier d'ailleurs : pour simplifier, j'appelle N le nombre 109601 et R la racine carrée de N.
Si A=B=R et C=1 on a alors en se souvenant que N=R*R
B / A = C² oui car R/R=1
√109601 / C = A oui car R/1=R
√109601 * C = B oui car R*1=R
109601 / C = √109601 * A oui car N/1=R*R
109601 / B = √109601 / C oui car N/R=R/1
109601 / C² = A² oui car N/1=R*R
Les résultats sont identiques si on remplace A et B par -R, et C par -1.
Le résultat est généralisable à tout N>0 et R racine carrée de N.
Enfin, si on ne cherche que des solutions différentes de 1, seule la solution C=-1 est correcte (donc A=B=-R).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Enigme mathématique - Equation à résoudre
Rebonjour hdci
Il semble que vous ayez raison pour la solution que vous proposez si l'on se place dans la perspective du problème tel que je l'avais formulé initialement et sans doute de façon non suffisamment précise.
Vos justes observations et les résultats que vous apportez m'obligent donc à revoir la formulation du problème en posant des conditions beaucoup plus précises. En effet le résultat que vous avez apporté (et qui est juste quand on se situe dans le cadre la formulation initiale) n'est pas celui que j'attends.
Il existe un résultat beaucoup plus intéressant encore que l'on sera peut-être en mesure d'obtenir avec la nouvelle formulation que je vous propose. Dans tous les cas je vous remercie pour vos réponses.
Il semble que vous ayez raison pour la solution que vous proposez si l'on se place dans la perspective du problème tel que je l'avais formulé initialement et sans doute de façon non suffisamment précise.
Vos justes observations et les résultats que vous apportez m'obligent donc à revoir la formulation du problème en posant des conditions beaucoup plus précises. En effet le résultat que vous avez apporté (et qui est juste quand on se situe dans le cadre la formulation initiale) n'est pas celui que j'attends.
Il existe un résultat beaucoup plus intéressant encore que l'on sera peut-être en mesure d'obtenir avec la nouvelle formulation que je vous propose. Dans tous les cas je vous remercie pour vos réponses.
Re: Enigme mathématique - Equation à résoudre
Bonjour
toutes ces équations se ramènent juste à poser
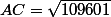 et
et 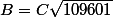
deux équations trois inconnues
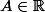 - {tous les éléments que vous ne voulez pas}
- {tous les éléments que vous ne voulez pas}
puis calculer B et C avec le A que vous vous donnez
Exemple
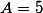
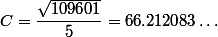
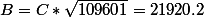
toutes ces équations se ramènent juste à poser
deux équations trois inconnues
puis calculer B et C avec le A que vous vous donnez
Exemple
Re: Enigme mathématique - Equation à résoudre
Exact ;
il semble que quand j'ai réduit à trois équations
J'ai en fait inversé B et C dans la troisième, issue de la cinquième initiale
109601 / B = √109601 / C
Du coup la troisième est en fait
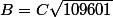
et se déduit des deux premières.
il semble que quand j'ai réduit à trois équations
hdci a écrit:On peut donc conserver les trois équations suivantes
J'ai en fait inversé B et C dans la troisième, issue de la cinquième initiale
109601 / B = √109601 / C
Du coup la troisième est en fait
et se déduit des deux premières.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Enigme mathématique - Equation à résoudre
Peut-être que tu as inversé ...
Mais peut-être pas.
Coinroad a modifié son premier message, en changeant les 6 équations, ce qui fait que la discussion n'a plus aucune cohérence.
Mais peut-être pas.
Coinroad a modifié son premier message, en changeant les 6 équations, ce qui fait que la discussion n'a plus aucune cohérence.
Re: Enigme mathématique - Equation à résoudre
lyceen95 a écrit:
Coinroad a modifié son premier message, en changeant les 6 équations, ce qui fait que la discussion n'a plus aucune cohérence.
lol je me disais aussi c'est un peu trop facile
pour une fois que j'avais un sujet simple pour aider quelqu'un : c'est foiré!
bon bah le mieux pour moi c'est de bosser mes maths afin d'aider sur des sujets plus compliqués
Bon noël à vous : mangez buvez! moi j'ai des maths à travailler

Re: Enigme mathématique - Equation à résoudre
Bonjour à vous, non lyceen 95 les 6 équations sont les mêmes, j'ai juste rajouté les conditions liées aux valeurs. Effectivement quand on utilise un solveur du type Wofam on arrive à ce que vous décrivez
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
