Bonjour fatal_error et merci de ta participation
j'ai du mal à voir où tu veux en venir, je le repete
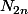
est le
nombre de fois où le solde est strictement positif ou devient nul par au-dessus comme tu dis. Par définition il est donc toujours supérieur ou égal à 0.
Mais tu as raison par symétrie il est évident que
=n)
, c'est exactement ce qu'à affirmer à juste titre lyceen95.
Par contre pour trouver la loi de probabilités et la variance, il va quand même falloir trouver les valeurs avec les probabilités associées, en tout cas, je ne sais pas faire autrement
Exemple pour

, il y a 4 tirages équiprobables :
Pile Pile (autrement dit
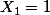
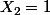
) donc les soldes sont
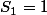
et
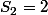
ce qui donne
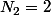
Pile Face (autrement dit
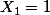
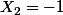
) donc les soldes sont
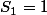
et
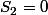
ce qui donne
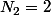
Face Pile (autrement dit
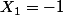
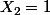
) donc les soldes sont
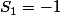
et
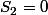
ce qui donne
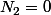
Face Face (autrement dit
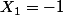
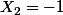
) donc les soldes sont
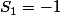
et
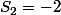
ce qui donne
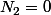
Au final, on trouve
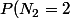=P(N_2=0)=1/2)
ainsi que
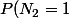=0)
ce qui nous donne la loi de probabilités et permet de vérifier
=2\times 1/2 + 0 \times 1/2 = 1)
=2^2 \times 1/2 + 0^2 \times 1/2 - 1^2= 1)
A vous de jouer pour

ou plus si affinités mais pas de panique, c'est un problème destiné à un concours du supérieur, c'est normal que ce soit "difficile"
Si vous voulez un indice, je peux vous donner le résultat à démontrer
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
