2^n divise 3^n-1
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 21 Juin 2006, 22:00
par aviateurpilot » 21 Juin 2006, 22:00
=y)
si
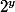
divise x et

ne divise pas x
voila ce qu'a fait yos si je l'ai bien compris
soit n de IN
si
=k)
alors
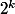
divise n et
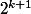
ne divisie pas n
donc il existe m de IN impair tel que
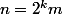
yos a trouve que
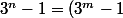\Bigprod_{i=0}^{k-1}(3^{2^im}+1))
or quelque soit i de [0;k-1]
=1)
et
=2)
donc
\Bigprod_{i=0}^{k-1}(3^{2^im}+1))=k+2)
donc
=k+2)
je pense que yos a fait ça,
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Juin 2006, 22:10
par yos » 21 Juin 2006, 22:10
Pour les valuations c'est plutôt

qui est multiple de 4 (et pas de 8) et on le voit en écrivant
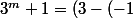)(3^{m-1}-3^{m-2}+3^{m-3}-...+1))
car m est impair. Le premier facteur est 4 et le second est une somme d'un nombre impair de nombres impairs.
Alors que

est de valuation 1 (même preuve).
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 21 Juin 2006, 22:12
par aviateurpilot » 21 Juin 2006, 22:12
pour que

divise
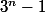
il faut que
\ge n)
donc d'apres ce que yos a trouvé
+2\ge n)

or si k\ge3

donc il ne rest que verifier par 1,2,
tous ca si est vrai si
=k+2)
vrai
or n=4 est une solution
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juil 2006, 23:34
par aviateurpilot » 04 Juil 2006, 23:34

divise
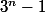
il existe y de N tel que
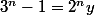
n=0 et n=1 sont des solutions
si n>1, on a
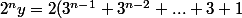)
donc

est pair
et puisque c'est une somme de n nombres impair donc n et pair (n=2k)
donc

divise
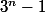

divise
(3^k-1))
=a)
et
=b)
avec

et on a
=PGCD(3^k+1;2)=2)
donc a=1 ou b=1 donc

ou

par suite
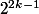
divise

ou

donc

dans les 2 cas.
et on a

si


donc

si on verifie avec k de {0,1,2} on trouve que pour n=0 et n=2 ;

divise
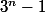
donc S={0,1,2}:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités