2^n divise 3^n-1
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Juin 2006, 01:02
par aviateurpilot » 17 Juin 2006, 01:02
salut les amis
voila un exo pour vous
Trouver tous les entiers n strictement positifs pour lesquels

divise
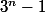
merci d'avances pour vos réponces
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 19 Juin 2006, 16:37
par aviateurpilot » 19 Juin 2006, 16:37
j'ai trouvé que n dois etre pair
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 19 Juin 2006, 16:51
par aviateurpilot » 19 Juin 2006, 16:51
en fin j'ai trouvé la solution
je te laisse chercher mikou
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 19 Juin 2006, 19:08
par Mikou » 19 Juin 2006, 19:08
;) jai demontrer que la seule valeure de n impair verifiant cela est 1, n n'est donc pas forcement impair ! de plus il faut trouver un ensemble et tt les nb pairs ne son pas solution :happy3:
bref il ne me reste 'plus' que les cas avec n pair
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 19 Juin 2006, 19:52
par BiZi » 19 Juin 2006, 19:52
Bonjour,
C'est pareil pour moi... Après ca j'ai fait n=2p d'où 3^n -1=(3^p+1)(3^p-1) mais je ne trouve aucune condition particulière sur p, même avec les suites géométriques, la méthode que j'avais utilisée pour prouver que n était pair. Un indice par pitié! :mur:
-
Jacques Lavau
- Membre Relatif
- Messages: 118
- Enregistré le: 19 Juin 2006, 00:19
-
 par Jacques Lavau » 19 Juin 2006, 22:06
par Jacques Lavau » 19 Juin 2006, 22:06
Déjà trois solutions : n = 1 ; 2 ; 4.
Pas trouvé de méthode générale.
0, 3, 5, 6 ne conviennent pas.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 19 Juin 2006, 22:14
par aviateurpilot » 19 Juin 2006, 22:14
moi j'ai trouvé la solution mais je vai pas la posté, je vous laisse chercher
bizi a écrit: Un indice par pitié!
1er indice
pgcd(3^p+1,3^p-1)=2
si tu veus un autre indice dis le
-
Jacques Lavau
- Membre Relatif
- Messages: 118
- Enregistré le: 19 Juin 2006, 00:19
-
 par Jacques Lavau » 19 Juin 2006, 22:22
par Jacques Lavau » 19 Juin 2006, 22:22
n supérieur à 1 implique que 3^n - 1 est divisible par 4. Preuve par le binôme :
3^n - 1 = (3-1)(3^n-2 + etc .. + 1)
et la symétrie du terme entre parenthèse, avec coefficient central toujours pair.
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 20 Juin 2006, 08:44
par Mikou » 20 Juin 2006, 08:44
Est tu sur de ta demo avionpilote ? La mienne montre bien que le seul n impair est 1, je vais traiter le cas n pair :happy3:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Juin 2006, 12:14
par aviateurpilot » 20 Juin 2006, 12:14
mikou a écrit:Est tu sur de ta demo aviateurpilot
oui, je t'ai dis l'autre fois que je ne me deconnecterais pas avant de trouver la solution
tu veus que je la poste ?
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 20 Juin 2006, 12:23
par Mikou » 20 Juin 2006, 12:23
non, mais tu dis avoir demontrer qu'il nexiste aucun entier impair verifiant lequation, or je t'ai di avoir demontrer qu'il en existe un seul a savoir 1.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Juin 2006, 12:28
par yos » 20 Juin 2006, 12:28
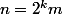
avec m impair.
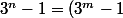(3^m+1)(3^{2m}+1)(3^{4m}+1)...(3^{2^{k-1}m}+1))
.
On regarde alors la valuation 2-adique des facteurs. Elle vaut 1 le plus souvent.
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 20 Juin 2006, 12:33
par Mikou » 20 Juin 2006, 12:33
Et avec des outils de term s :lol4: ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Juin 2006, 12:43
par aviateurpilot » 20 Juin 2006, 12:43
je suis en terminal
et j'ai trouvé une solution avec des outils de term s
je n'ai utiliser que le 1er indice que j'ai donné
et une différence de 2 quantités qui doit etre positive
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Juin 2006, 13:07
par yos » 20 Juin 2006, 13:07
Qu'est-ce qui n'est pas un outil de terminale? La valuation p-adique? C'est une notion sous-jacente à la décomposition en facteurs premiers : cette décomposition est unique pour un entier donné n; l'exposant d'un premier p qui y figure s'appelle la valuation p-adique de n et se note
)
.
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 20 Juin 2006, 13:09
par Mikou » 20 Juin 2006, 13:09
d'accord, merci pour lexplication :happy3:
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Juin 2006, 13:33
par BiZi » 20 Juin 2006, 13:33
Je crois que j'ai trouvé! :id: Merci pour l'indice ca m'a mis indirectement sur la voie! :++:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Juin 2006, 13:51
par aviateurpilot » 20 Juin 2006, 13:51
bizi a écrit:Merci pour l'indice ca m'a mis indirectement sur la voie
pas de koi
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Juin 2006, 20:13
par yos » 21 Juin 2006, 20:13
Il me semble que la méthode que j'ai donnée plus haut est pas mal. Elle donne plus de chose :
=v_2(n)+2)
.
Cependant je veux bien voir les autres méthodes.
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 21 Juin 2006, 21:22
par BiZi » 21 Juin 2006, 21:22
Euh yos tu pourrais pas stp expliciter un peu ta solution? Parce que je suis un peu paumé là...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités