DIFFICILE
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 14 Aoû 2025, 01:11
par MMu » 14 Aoû 2025, 01:11
Soit
)
un polynôme de degré

à variable et coefficients réels, tel que
|\leq 1)
Montrer que
|\leq 2^{n-1}x ^n)

-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 15 Aoû 2025, 17:05
par MMu » 15 Aoû 2025, 17:05
Mea culpa (erreurs de rédaction) : manifestement il faut
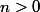
et


-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 16 Aoû 2025, 11:37
par ComeDuRondeau » 16 Aoû 2025, 11:37
MMu a écrit:Soit
)
un polynôme de degré

à variable et coefficients réels, tel que
|\leq 1)
Montrer que
|\leq 2^{n-1}x ^n)

J'ai essayé en exprimant

dans des bases adaptées au problèmes. Avec les polynômes de Tchebychev ça a l'air prometteur ; on peut exprimer les coefficients de

dans cette base comme les coefficients de Fourier de
))
et obtenir une majoration de ceux-ci et de leurs sommes grâce aux hypothèses et aux propriétés des polynômes de Tchebychev mais je n'ai pas réussi à aboutir.
Avec différents choix d'abscisses pour les bases d'interpolation de Lagrange on arrive à des majorations mais plus grosses que celles demandées

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Aoû 2025, 15:02
par Ben314 » 27 Aoû 2025, 15:02
Salut,
J'ai l'impression que le "plus grand" polynôme de degré

vérifiant l'hypothèse est le

-ième polynôme de Tchebychev

: si

est tel que
\!\in\![-1,1])
alors
\!\leqslant\!T_n(x))
.
Si c'est bien le cas, on en déduit facilement l'inégalité demandée, mais, pour le moment, je n'ai pas la preuve de ce résultat...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Aoû 2025, 22:51
par Ben314 » 30 Aoû 2025, 22:51
En fait, c'est assez immédiat : vu les

oscillations entre -1 et 1 que fait

sur l'intervalle

, tout polynôme

tel que
\!\subset\![-1,1])
est tel que l'équation
\!=\!T_n(x))
admet au moins

racines (comptées avec ordre de multiplicité) sur

. Donc, si

est de degrés

, il n'y a pas de racines sur
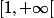
et on en déduit bien que
\!\leqslant\!T_n(x))
pour tout

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités

un polynôme de degré
à variable et coefficients réels, tel que
|\leq 2^{n-1}x ^n)