J'ai un exercice du Maths dont je n'est pas la solution..Est-ce que vous pouvez m'aider?
sois x et y 2 nombres reels qui verifient : 1;) x^2 +y^2-xy;)2 montrez que :
I).2/9;) x^4+y^4;)8
II).montrez que quelque sois n;)3 on a : x^2n + y^2n ;) 2/3^2n
merci d'avance mes amis :marteau:
Inegalité d'olympiade tres difficile :)
8 messages
- Page 1 sur 1
Salut,
Pour le premier, on s'en sort aisément par des moyens trés rudimentaires :
On pose et
et  donc
donc 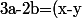^2\geq 0) et
et 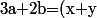^2\geq 0) .
.
L'hypothèse s'écrit et on doit encadrer
et on doit encadrer  .
.
On a\leq b\leq\min(\frac{a}{2}\,;\,a-1)) et
et  .
.
Comme alors
alors ^2=\frac{1}{2}a^2\geq \frac{1}{2} \left(\frac{2}{3}\right)^2=\frac{2}{9}) .
.
(avec égalité ssi et
et  , c'est à dire
, c'est à dire  )
)
Si alors
alors  .
.
Si alors
alors  donc
donc ^2=8-(4-a)^2\leq 8)
(avec égalité ssi et
et  , c'est à dire
, c'est à dire  )
)
Mais je suis pas certain qu'on y arrive aussi simplement pour le cas général (mais ça risque fortement de donner des idées...)
Pour le premier, on s'en sort aisément par des moyens trés rudimentaires :
On pose
L'hypothèse s'écrit
On a
Comme
(avec égalité ssi
Si
Si
(avec égalité ssi
Mais je suis pas certain qu'on y arrive aussi simplement pour le cas général (mais ça risque fortement de donner des idées...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour l'autre côté de l'inégalité, je dirais que c'est faisable avec la même méthode, càd factoriser ^2-x^4-y^4) .
.
Pour la généralisation, ça se fait facilement par récurrence . On montre que pour tout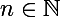 :
: 
Pour n=0 c'est pas intéressant, pour n=1 :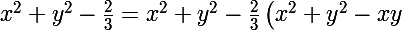 + \frac{2}{3} \left(x^2+y^2-xy-1\right) = \frac{1}{3}\left(x+y\right)^2 + \frac{2}{3}\left(x^2+y^2-xy-1\right) \geq 0) .
.
On suppose que l'inégalité est vraie pour un certain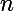 .
.
Il est clair que\left(x^{2n} - y^{2n}\right) \geq 0)

 \geq \left(x^2+y^2\right)\left(x^{2n}+y^{2n} \right))
Mais et par hypothèse de récurrence
et par hypothèse de récurrence  , d'où la conclusion .
, d'où la conclusion .
Sur ce, je retourne à mes révisions :happy3:
Pour la généralisation, ça se fait facilement par récurrence . On montre que pour tout
Pour n=0 c'est pas intéressant, pour n=1 :
On suppose que l'inégalité est vraie pour un certain
Il est clair que
Mais
Sur ce, je retourne à mes révisions :happy3:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
