Soit
1) Quel est le déterminant de la matrice
Par exemple, pour
2) D'où vient ce déterminant ?
Déterminant
12 messages
- Page 1 sur 1
Déterminant
par Ben314 » 10 Déc 2010, 15:51
Salut,
Soit
et, pour tout 
, 
(conventionellement 
donc 
)
1) Quel est le déterminant de la matrice_{0\leq i,j< n})
(donc de taille 
) ?
Par exemple, pour
, 
2) D'où vient ce déterminant ?
Soit
1) Quel est le déterminant de la matrice
Par exemple, pour
2) D'où vient ce déterminant ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Doraki » 10 Déc 2010, 16:52
T'es sur que la réponse à 2) trivialise pas la réponse à 1) ?
Pour n=1,2,3, il me semble bien que ça fait le Produit des (xi-xj)².
Pour n=1,2,3, il me semble bien que ça fait le Produit des (xi-xj)².
par Ben314 » 10 Déc 2010, 19:28
Vu l'endroit d'où j'ai sorti ce determinant (mais il ne sort surement pas que d'un seul endroit... :doh: ), je n'en déduit pas directement sa valeur...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Nightmare » 10 Déc 2010, 19:50
J'ai rien du tout :happy3:
J'ai jamais été doué en astuce pour calculer les déterminant, mais généralement je m'en sortais toujours bien à la bourrin. Et là, à la bourrin, ça devient vite horrible...
Si tu veux poster un indice en blanc, quitte à ce que je le lise plus tard, ne t'en prive pas !
J'ai jamais été doué en astuce pour calculer les déterminant, mais généralement je m'en sortais toujours bien à la bourrin. Et là, à la bourrin, ça devient vite horrible...
Si tu veux poster un indice en blanc, quitte à ce que je le lise plus tard, ne t'en prive pas !
par Ben314 » 10 Déc 2010, 21:06
Bon, puisque tout le monde insiste lourdement, je vais me fendre d'un énorme indice :
J'ai la soluce à la question 2) (forcément.... :marteau:) mais j'ai pas la solution à la question 1) (bien que je sois convaincu du bien fondé de la conjecture de Doraki).
Bon, pour la 2), je donne une "indic" : ce type de matrice est archi connu dans un certain domaine des maths lorsque n est "assez grand" mais que l'on ne considère que la matrice 2x2 de la forme sus-mentionnée.
Par exemple de la réponse au 2), je déduit trés facilement que si on considère une matrice de la forme sus mentionnée mais de taille strictement plus grande que n alors le déterminant est nul.
Bon, si personne ne trouve la réponse au 2), je la donnerais (pour qu'on m'aide à trouver la réponse au 1)... :zen:)
J'ai la soluce à la question 2) (forcément.... :marteau:) mais j'ai pas la solution à la question 1) (bien que je sois convaincu du bien fondé de la conjecture de Doraki).
Bon, pour la 2), je donne une "indic" : ce type de matrice est archi connu dans un certain domaine des maths lorsque n est "assez grand" mais que l'on ne considère que la matrice 2x2 de la forme sus-mentionnée.
Par exemple de la réponse au 2), je déduit trés facilement que si on considère une matrice de la forme sus mentionnée mais de taille strictement plus grande que n alors le déterminant est nul.
Bon, si personne ne trouve la réponse au 2), je la donnerais (pour qu'on m'aide à trouver la réponse au 1)... :zen:)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Doraki » 10 Déc 2010, 21:07
Si j'appelle ;)1 = (x1+x2+...+xn), ;)2 = - (x1x2+x2x3+...), ..., ;)n = (-1)^(n-1) (x1x2...xn),
alors il me semble qu'on a que pour tout k,
le produit scalaire (Sk,S(k+1),...,S(k+n-1)).(;)n,...,;)2,;)1) vaut S(k+n).
en effet, modulo permutation des xi, chaque monôme est de la forme x1x2...xm x(m+1)^(k+n-m),
et si m>0, ils proviennent tous à la fois d'un ;)m * S(k+n-m) et d'un ;)(m+1) * S(k+n-m-1).
Comme le signe change, ça s'annule.
Oh et il y en a pas avec m=n paske y'a pas assez de place.
Du coup, il reste seulement les monômes de la forme x1^(k+n) venant de S(k+n-1)*;)1.
Donc si on note X le vecteur (;)n,...,;)2,;)1), A X = (Sn, Sn+1,...,S(2n-1)).
Bon au début je voulais éviter de faire d'autres trucs compliqués pour prouver la suite, mais il me semblait qu'en dérivant par rapport à x1, et qu'en faisant x1=x2, on obtenait ptetre A (dX/dx1) = d((Sn...S(2n-1))/dx1 - dA/dx1 X = 0, ce qui montrerait que le déterminant est divisible par (x2-x1)².
(en tout cas, j'crois que dX/dx1 est un bon vecteur annulateur de A dans le cas x1=x2).
A fortiori ça me paraît pas tellement simple de le montrer.
alors il me semble qu'on a que pour tout k,
le produit scalaire (Sk,S(k+1),...,S(k+n-1)).(;)n,...,;)2,;)1) vaut S(k+n).
en effet, modulo permutation des xi, chaque monôme est de la forme x1x2...xm x(m+1)^(k+n-m),
et si m>0, ils proviennent tous à la fois d'un ;)m * S(k+n-m) et d'un ;)(m+1) * S(k+n-m-1).
Comme le signe change, ça s'annule.
Oh et il y en a pas avec m=n paske y'a pas assez de place.
Du coup, il reste seulement les monômes de la forme x1^(k+n) venant de S(k+n-1)*;)1.
Donc si on note X le vecteur (;)n,...,;)2,;)1), A X = (Sn, Sn+1,...,S(2n-1)).
Bon au début je voulais éviter de faire d'autres trucs compliqués pour prouver la suite, mais il me semblait qu'en dérivant par rapport à x1, et qu'en faisant x1=x2, on obtenait ptetre A (dX/dx1) = d((Sn...S(2n-1))/dx1 - dA/dx1 X = 0, ce qui montrerait que le déterminant est divisible par (x2-x1)².
(en tout cas, j'crois que dX/dx1 est un bon vecteur annulateur de A dans le cas x1=x2).
A fortiori ça me paraît pas tellement simple de le montrer.
par Ben314 » 10 Déc 2010, 22:39
Bon, je vend la mèche sur le 2) :
J'ai eu l'idée suite à un post d'un étudiant demandant comment on fait pour approximer un nuage de points (xi,yi) par une fonction de degrés 3 et je lui ait dit de faire des "moindres carrés" dont l'étude consiste à chercher le minimum de la fonction :\mapsto\sum_{i=1}^n(ax_i^3+bx_i^2+cx_i+d-y_i)^2)
Le système correspondant à dire que les dérivées partielles en
doivent être nulles est en fait linéaire en et la matrice correspondante est du type sus mentionné.
En fait, si on veut voir le truc de façon plus joli, pour
fixés, on regarde l'application =\sum_{i=1}^n\left(P(x_i)\right)^2)
qui est clairement une forme quadratique positive sur 
de forme bilinéaire associée =\sum_{i=1}^nP(x_i)Q(x_i))
La matrice associée dans la base
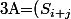est donc _{0\leq i,j\leq d})
(l'énoncé correspondant trés précisément au cas où 
).
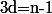
Le déterminant de la matrice est nul ssi la forme quadratique est dégénérée ce qui, vu qu'elle est positive, équivaut à l'existence d'un polynôme
non nul tel que =0)
.
Evidement, cette dernière condition équivaut au fait que le nombre de
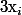distincts doit être 
.
Cela montre que :
Si
le determinant est toujours nul.
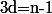
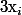
Si (cas de l'énoncé) le déterminant est nul ssi deux (ou plus) des sont égaux donc on peut factoriser tout les )
avec 
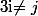
(mais ça ne donne pas la solution complète...)
Si par exemple
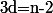
, le determinant est nul ssi il existe 
distincts tels que 
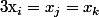
OU BIEN s'il existe 
distincts tels que 
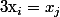
et 
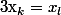
mais je ne pense pas qu'on puisse en déduire une factorisation (???)
J'ai eu l'idée suite à un post d'un étudiant demandant comment on fait pour approximer un nuage de points (xi,yi) par une fonction de degrés 3 et je lui ait dit de faire des "moindres carrés" dont l'étude consiste à chercher le minimum de la fonction :
Le système correspondant à dire que les dérivées partielles en
En fait, si on veut voir le truc de façon plus joli, pour
La matrice associée dans la base
Le déterminant de la matrice est nul ssi la forme quadratique est dégénérée ce qui, vu qu'elle est positive, équivaut à l'existence d'un polynôme
Evidement, cette dernière condition équivaut au fait que le nombre de
Cela montre que :
Si
Si
Si par exemple
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 10 Déc 2010, 22:54
En fait, en réfléchissant un peu plus (comme quoi, des fois, ça sert... :lol3:), le déterminant doit être positif vu que la forme quadratique l'est et cela implique que les (xi-xj) apparaissent à une puissance paire.
Sauf erreur, vu le degré du polynôme que l'on cherche, cela signife qu'on l'a trouvé à une constante multiplicative (positive) prés et ça doit pas être sorcier (en cherchant le coeff d'un monome bien choisi) de montrer que le coeff en question est 1.
Ce qui serait marrant ça serait de relier la méthode "forme quadratique" à ce qu'a commencé à faire Doraki. Son "vecteur" correspond en fait au polynôme P=(X-x1)(X-x2)...(X-xn) dont on a "enlevé" le terme dominant X^n...
Sauf erreur, vu le degré du polynôme que l'on cherche, cela signife qu'on l'a trouvé à une constante multiplicative (positive) prés et ça doit pas être sorcier (en cherchant le coeff d'un monome bien choisi) de montrer que le coeff en question est 1.
Ce qui serait marrant ça serait de relier la méthode "forme quadratique" à ce qu'a commencé à faire Doraki. Son "vecteur" correspond en fait au polynôme P=(X-x1)(X-x2)...(X-xn) dont on a "enlevé" le terme dominant X^n...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Doraki » 13 Déc 2010, 13:35
Non en fait mon truc c'était juste un moyen compliqué de dire que si un vecteur P correspond à un polynôme dont a est racine, le produit scalaire <(1,a,a²...,a^(n-1)) , P> est nul.
(j'avais pas identifié que je faisais un truc aussi reconnaissable)
Quand on augmente le nombre de xi sans changer la taille de la matrice, je suis pas sûr que ça se factorise toujours bien.
Par exemple pour 3 points et des polynômes de degré 1,
on a du (a²+b²+c²-ab-bc-ca) = (a+jb+j²c)(a+j²b+jc), qui est nul quand a,b,c sont en triangle équilatéral.
Pour 4 points et degré 2, ben ça donne un gros truc horrible de degré 4 en chaque variable et de degré total 6.
(j'avais pas identifié que je faisais un truc aussi reconnaissable)
Quand on augmente le nombre de xi sans changer la taille de la matrice, je suis pas sûr que ça se factorise toujours bien.
Par exemple pour 3 points et des polynômes de degré 1,
on a du (a²+b²+c²-ab-bc-ca) = (a+jb+j²c)(a+j²b+jc), qui est nul quand a,b,c sont en triangle équilatéral.
Pour 4 points et degré 2, ben ça donne un gros truc horrible de degré 4 en chaque variable et de degré total 6.
par Ben314 » 13 Déc 2010, 16:42
Effectivement,mais dans le cas d=1, n=3, je ne sais pas bien d'où provient la factorisation "miraculeuse" dans C du déterminant (tu l'as trouvé par le calcul uniquement ou tu as l'impression qu'il y a une "idée" derrière ?).
Si on regarde la "théorie théorique" (dans R) on sait juste que le déterminant est nul dans R ssi a=b=c
(et comme q n'est pas une forme hermitienne sur Cd[X], ben je sais plus dire grand chose dans C...
)
idem pour n=4 et d=2 : le gros merdier que l'on obtient, dans R, il est nul ssi les 4 variables au total n'ont pas plus de deux valeurs différentes, mais dans C ???
Ce que je trouve marrant, c'est que, toujours dans R, ça permet d'écrire un polynôme en 36 variables qui soit nuls ssi les 36 variables n'ont au plus que 25 valeurs différentes. On m'aurait à froid demandé de produire un tel polynôme, ben je sais pas comment j'aurais fait...
Question : un tel polynôme peut il exister sur C ? sur un corps quelconque ? Par exemple :
Si on regarde la "théorie théorique" (dans R) on sait juste que le déterminant est nul dans R ssi a=b=c
(et comme q n'est pas une forme hermitienne sur Cd[X], ben je sais plus dire grand chose dans C...
)idem pour n=4 et d=2 : le gros merdier que l'on obtient, dans R, il est nul ssi les 4 variables au total n'ont pas plus de deux valeurs différentes, mais dans C ???
Ce que je trouve marrant, c'est que, toujours dans R, ça permet d'écrire un polynôme en 36 variables qui soit nuls ssi les 36 variables n'ont au plus que 25 valeurs différentes. On m'aurait à froid demandé de produire un tel polynôme, ben je sais pas comment j'aurais fait...
Question : un tel polynôme peut il exister sur C ? sur un corps quelconque ? Par exemple :
(A mon avis, c'est de la géométrie algébrique, mais j'y connais quasi que dalle...)défi a écrit:Existe t'il un polynôme P(a,b,c,d) de C[a,b,c,d] qui s'annule ssi l'ensemble {a,b,c,d} est de cardinal inférieur ou égal à 2 ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Doraki » 13 Déc 2010, 17:13
Non y'en a pas.
Quand tu le regardes comme polynôme en d tu trouves que t'as un polynôme en d qui ne doit presque jamais s'annuler. Donc les coefficients devant d, d², etc son nuls pour presque tous a,b,c, donc ils sont nuls.
Pareil avec les autres variables, donc ton polynôme est constant ou nul, donc il existe pas.
La variété algébrique que tu veux obtenir n'est pas de la bonne dimension.
Il faut plusieurs polynômes pour engendrer l'idéal des polynômes qui s'annulent quand Card{a,b,c,d} <=2.
Les zéros du polynôme horrible qu'on obtient décrit les quadruplets (a,b,c,d) tels qu'il existe un polynôme Q de degré 2 tel que Q(a)²+Q(b)²+Q(c)²+Q(d)² = 0.
Si {a,b,c,d} = {a,b}, le Q qui convient est (X-a)(X-b).
Pour la factorisation miraculeuse bah elle est miraculeuse pour l'instant.
Pour info, le polynôme Q tel que Q(1)²+Q(j)²+Q(j²)² = 0 c'est X.
Les homothéties changent le triangle mais pas le polynôme Q,
et les translations/rotations agissent en même temps sur Q et sur le triangle.
Avec 4 points, l'ensemble des "formes" qui correspondent ça reste stable par les applications affines,
Mais cette fois-ci, y'en a plein.
Si on fixe un segment (a=0, b=1), et si on laisse c quelconque, alors d aura toujours 4 positions possibles.
Quand tu le regardes comme polynôme en d tu trouves que t'as un polynôme en d qui ne doit presque jamais s'annuler. Donc les coefficients devant d, d², etc son nuls pour presque tous a,b,c, donc ils sont nuls.
Pareil avec les autres variables, donc ton polynôme est constant ou nul, donc il existe pas.
La variété algébrique que tu veux obtenir n'est pas de la bonne dimension.
Il faut plusieurs polynômes pour engendrer l'idéal des polynômes qui s'annulent quand Card{a,b,c,d} <=2.
Les zéros du polynôme horrible qu'on obtient décrit les quadruplets (a,b,c,d) tels qu'il existe un polynôme Q de degré 2 tel que Q(a)²+Q(b)²+Q(c)²+Q(d)² = 0.
Si {a,b,c,d} = {a,b}, le Q qui convient est (X-a)(X-b).
Pour la factorisation miraculeuse bah elle est miraculeuse pour l'instant.
Pour info, le polynôme Q tel que Q(1)²+Q(j)²+Q(j²)² = 0 c'est X.
Les homothéties changent le triangle mais pas le polynôme Q,
et les translations/rotations agissent en même temps sur Q et sur le triangle.
Avec 4 points, l'ensemble des "formes" qui correspondent ça reste stable par les applications affines,
Mais cette fois-ci, y'en a plein.
Si on fixe un segment (a=0, b=1), et si on laisse c quelconque, alors d aura toujours 4 positions possibles.
par Ben314 » 13 Déc 2010, 18:13
Concernant la réponse dans C, ça ne m'étonne pas et, j'aurais du le savoir (la notion de dimension pour une variété algébrique fait normalement parti des trucs que j'ai vu à un moment donné... comme quoi en vieillissant... :cry:)
Aprés, concernant le cas n=4, d=2, je supputerais assez fort que l'on tombe sur un truc plus ou moins "connu" de géométrie (coniques ?) mais là j'ai pas trop le temps de chercher...
(je me le garde sous le coude pour les vacances de Noël...)
En tout cas, je trouve ça marrant qu'on puisse dire des choses aussi "rigolotes" en partant "bêtement" des formules d'interpolations par les moindres carrés...
L'autre truc que je me demandais, ça concernait le fait que, pour d=1, le déterminant divisé par n², ben c'est la variance des xi qui correspond plus ou moins à un truc "concret".
Est ce que pour d=2 (et en divisant par n³) ça correspond à quelque chose de connu ? de "concret" ?
Aprés, concernant le cas n=4, d=2, je supputerais assez fort que l'on tombe sur un truc plus ou moins "connu" de géométrie (coniques ?) mais là j'ai pas trop le temps de chercher...
(je me le garde sous le coude pour les vacances de Noël...)
En tout cas, je trouve ça marrant qu'on puisse dire des choses aussi "rigolotes" en partant "bêtement" des formules d'interpolations par les moindres carrés...
L'autre truc que je me demandais, ça concernait le fait que, pour d=1, le déterminant divisé par n², ben c'est la variance des xi qui correspond plus ou moins à un truc "concret".
Est ce que pour d=2 (et en divisant par n³) ça correspond à quelque chose de connu ? de "concret" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :