Défi géométrique (issu de la revue mathématique "Tangente")

[Timothé Lefebvre]

Salut tout le monde

Je vous propose un défi géométrique à résoudre, publié dans la revue mathématique "Tangente" (numéro 125 je crois).

Voici l'énoncé :

On donne quatre droites strictement parallèles , , et telles que soit entre et , et entre et , et une perpendiculaire à ces quatre droites qui coupe en et en .

On demande de construire, lorsque c'est possible, à l'aide de la règle et du compas, un point de et un point de tels que .

Voici le schéma ci-dessous, dessiné avec GeoGebra.

[url="http://img193.imageshack.us/i/defigeo1t.png/"][/url]


[color=black]Amusons-nous bien :zen:

Tim
[/color]

[Timothé Lefebvre]

Je ne peux pas croire que personne ne soit intéressé !

Imod que fais-tu ?!

[Imod]

Imod que fais-tu ?!

Une très grosse journée qui n'est que le début d'une très grosse semaine hum:

Mais ton problème est intéressant et je ne manquerai pas d'y jeter un coup d'oeil chaque fois que j'en aurai l'occasion :we:

Imod

[Timothé Lefebvre]

Ah me voilà rassuré :)
Bien sûr d'autres peuvent se pencher dessus mais Imod est un peu le Mage du temple "Enigmes" !

[nuage]

Salut,
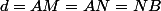
il est assez facile de montrer que ne dépend que de , et . L'ordre n'intervient pas.
Après ça, comme je suis un peu bourrin, j'ai calculé :
je trouve une solution unique

Ce qui est manifestement constructible à la règle et au compas à partir de , et . :zen:
Mais c'est encore assez loin d'une solution pratique.
Enfin on sait au moins qu'il y a toujours une solution et qu'elle est unique.

[Timothé Lefebvre]

C'est exact :++:

Il y a bien sûr une équation plus simple :P