Combinatoire

[lapras]

Bonsoir,
je poste ce sujet dans la partie énigme, même si l'exercice est un exercice d'OIM, car c'est plutôt de la combinatoire.
Soit S et F deux sommets opposés d'un octogone. Un compteur démarre en A et à chaque seconde se déplace sur les sommets adjacents aléatoirement. Le processus s'arrête quand il atteint E. Soi a_n le nombre de chemins e durée n secondes que le compteur utilise pour aller de A à E.
Montrer que :
Pour tout n
a_(2n-1) = 0


Bonne chance !

[lapras]

Je peux mettre des indices si vous le voulez. N'ayez pas peur, même si la formule est complexe, la démontrer est moins dur que ça en a l'air. :++:

[scelerat]

Soit S et F deux sommets opposés d'un octogone.

S et F, ou A et E ? :hum:

[scelerat]

En un nombre impair de secondes, il est evident qu'on ne peut couvrir un nombre pair de trajets. Ensuite, en deux secondes, on remarque qu'on revient au point de depart ou qu'on se trouve deux sommets plus loin. On peut donc se limiter a un carre ACEG, et peut-etre regarder la projection du trajet sur sa diagonale AE ?

[ThSQ]

Çà sent la récurrence et l'équation caractéristique à 10 km !

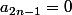
c'est clair comme ça a été dit.

En différenciant suivant que l'on vient de la droite ou la gauche ou de S il vient :

a(2n+2) = 4a(2n) + 2a(n-2)
a(2) = 0, a(4) = 2

Ca se résout classiquement (bizarre d'ailleurs comme exo OIM ...) avec l'équation caractéristique ou par récurrence.

[lapras]

Exact ThSQ, il fallait trouver une relation récurrente pour les a_n. Nous, en cour, on s'est aidé de suites pour chaque sommet on créait une suite et en résolvant le systeme de quatre équations on trouvait ta relation avec les a_n.
Puis avec l'équation caractéristique c'est fini. :)

[ThSQ]

en cour

En cour de récré ?

Sérious, tu as des cours sur les pb d'olympiades ?

[Imod]

Sérious, tu as des cours sur les pb d'olympiades ?

Sérieusement , quand on voit certaines inégalités ( par exemple ) des olympiades , on peut se dire qu'on est à mille lieues de l'esprit et du contenu des programmes de terminale et qu'envoyer un élève aux qualifications des olympiades sans un minimum d'entrainement , c'est sûrement l'envoyer à l'abattoir .

Imod

[ThSQ]

Entièrement d'accord ! Le cas des inégalités est édifiant. Sans préparation c'est impossible de faire quoi que ce soit là-dessus.

Moi je m'étais préparé tout quasi-seul et c'est pas évident .... :hum:
Si lapras peut avoir des cours c'est super pour lui :++:

[lapras]

salut,
oué j'ai des cours en fait c'est à la faq d'orsay (la où j'habite) il y a quelqun qui donne des exercices tous les samedis et qui nous aide à les résoudre. De plus, c'est gratuit, et puis c'est vachement interessant, surtout qu'on fait en particulier de l'arithmétique. Mais les inégalités, y'a pas moyens, faut les apprendre, il nous a donné (gratuitement encore !) des polycopiés d'animath imprimés, comme ca on peut les lire a tout moment. :++:
Dis moi, thSQ, as tu fait les olympiades internationales ?

[rafbh]

SALUT
Pouvons nous d'une facon ou d'une autre avoir ces cours??
C'est tellement interessant surtout quand c'est toujours la galère quand je m'attaque à un OIM.
Merci

[lapras]

salut,
a moins d'habiter a orsay ca risque d'être difficile pour le moment.
Mais justement, on va peut être installer des webcams dans la salle et les mettre en ligne sur ,le net pour que ceux qui ne peuvent pas assister aux cours puissent quand même regarder.
c'est pas fait mais c'es en projet.

[raito123]

Ouais ça doit être chouette!!!