
Combinatoire
16 messages
- Page 1 sur 1
Re: Combinatoire
Salut,
Sauf erreur,\!=\!\lfloor\varphi n\rfloor) (partie entière) où
(partie entière) où ) est le "nombre d'or".
est le "nombre d'or".
Sauf erreur,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Si on prend \!=\!\lfloor\varphi n\rfloor) tes deux égalités équivalent respectivement (après de mini calculs) à
tes deux égalités équivalent respectivement (après de mini calculs) à \!<\!\varphi n) et
et \!<\!\varphi n\!+\!\varphi\!-\!1) qui sont vraies vu que
qui sont vraies vu que \!<\!\varphi n\!<\!f(n)\!+\!1) (avec des inégalités strictes car
(avec des inégalités strictes car  ).
).
Et pour montrer que c'est l'unique solution, il suffit de dire que, si\!=\!\lfloor\varphi n\rfloor) pour tout
pour tout  alors pour ces
alors pour ces  là, on a
là, on a \!=\!f(n)\!+\!1) ou
ou 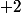 donc
donc  est un
est un ) ou (inclusif) un
ou (inclusif) un \!+\!1) donc au moins une des deux formules donne la valeur de
donc au moins une des deux formules donne la valeur de ) : il n'y a donc pas le choix.
: il n'y a donc pas le choix.
Et pour montrer que c'est l'unique solution, il suffit de dire que, si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Désolé , je n’ai pas été clair , ma question était comment on arrive à la solution .. mais peut être ce n’est pas important .. 

Re: Combinatoire
Perso, j'ai commencé par me dire que la fonction cherchée devait être proche d'une fonction réelle  telle que
telle que \big)\!=\!F(x)\!+\!x) qui admet une solution linéaire évidente, à savoir
qui admet une solution linéaire évidente, à savoir \!=\!\lambda x) avec
avec  . Ensuite, j'ai regardé l'écart entre
. Ensuite, j'ai regardé l'écart entre  et
et  pour les premières valeurs entières (avec un tableur) et conjecturé le résultat.
pour les premières valeurs entières (avec un tableur) et conjecturé le résultat.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
En plus (beaucoup plus) bourrin on peut chercher les premiers termes (une bonne vingtaine) puis voir si cela figure dans l'encyclopédie des suites OEIS
et on trouve :
https://oeis.org/A000201
On voit que cette suite intervient dans pas mal de situations pour ceux qui maitrisent l'anglais et les maths...
et on trouve :
https://oeis.org/A000201
On voit que cette suite intervient dans pas mal de situations pour ceux qui maitrisent l'anglais et les maths...
Re: Combinatoire
Cette suite, je la connaissait aussi du fait du théorème de je-sais-plus-qui qui dit que si 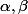 sont deux irrationnels >0 alors les parties entières de
sont deux irrationnels >0 alors les parties entières de  et
et 
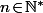 donnent une partition de
donnent une partition de 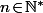 .
.
Donc, vu que les termes qui ne sont pas dans ta suite (f(n)), c'est les parties entières de
les termes qui ne sont pas dans ta suite (f(n)), c'est les parties entières de n) , c'est à dire en fait, les n+f(n) : tout entier naturel non nul est un f(n) ou (exclusif) un n+f(n).
, c'est à dire en fait, les n+f(n) : tout entier naturel non nul est un f(n) ou (exclusif) un n+f(n).
Donc, vu que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Tient, à titre de mini énigme :
Est-ce la seule fonction de telle que tout
telle que tout  soit un
soit un ) ou (exclusif) un
ou (exclusif) un ) ?
?
Est-ce la seule fonction de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Il me semble que ce n’est pas la seule.
La fonction=1) vérifie bien la demande si j’ai bien compris la question ..
vérifie bien la demande si j’ai bien compris la question .. 
La fonction

Re: Combinatoire
La question, c'est ça :
Déterminer toutes les fonctions telles que les deux ensembles
telles que les deux ensembles 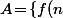:n\!\in\N^*\}) et
et :n\!\in\N^*\}) forment une partition de
forment une partition de 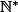 . (Donc
. (Donc  constante, ça ne marche pas du tout.)
constante, ça ne marche pas du tout.)
Déterminer toutes les fonctions
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Ben314 a écrit:La question, c'est ça :
Déterminer toutes les fonctionstelles que les deux ensembles
et
forment une partition de
. (Donc
constante, ça ne marche pas du tout.)
Il y a là une subtilité que je ne saisis pas , puisque pour

Re: Combinatoire
Oui, c'est effectivement moi qui suis complètement à coté de la plaque : dans ma tête, B était aussi fini . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Combinatoire
Ben314 a écrit:La question, c'est ça :
Déterminer toutes les fonctionstelles que les deux ensembles
et
forment une partition de
.
Bonjour
Si on prend f définie sur
B est l'ensemble des entiers pairs non nuls et A celui des entiers impairs
mais il doit y en avoir d'autres...
Re: Combinatoire
Oui, j'ai l'impression que, tel quel, l'énoncé laisse trop de liberté. Peut-être rajouter "f injective", voire "f strictement croissante" rendrait le truc plus intéressant.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
