Combinaisons
17 messages
- Page 1 sur 1
Combinaisons
Bonsoir
Voici un petit problème que j'ai rencontré en programmation de jeu et dont je n'arrive pas à trouver de solution simple.
Chacun sait qu'il y a C(n,p) façon de choisir p éléments parmi n.
Je cherche un fonction simple qui permettrait de retrouver une disposition à partir de son numéro.
Je m'explique.
Il y a par exemple 10 façons de positionner 2 bleus parmi 5 :
:triste: :triste: :hein: :hein: :hein:
:triste: :hein: :triste: :hein: :hein:
:triste: :hein: :hein: :triste: :hein:
:triste: :hein: :hein: :hein: :triste:
:hein: :triste: :triste: :hein: :hein:
etc ...
On affecte à chaque "façon" un numéro de 1 à 10. Peut on facilement retrouver la position des 2 bleus à partir de ce simple numéro ? Soit ici une fonction de [1,10] vers [1,5]x[1,5]
Je cherche bien sur une formule dans le cas général p,n.
Merci de votre collaboration.
Voici un petit problème que j'ai rencontré en programmation de jeu et dont je n'arrive pas à trouver de solution simple.
Chacun sait qu'il y a C(n,p) façon de choisir p éléments parmi n.
Je cherche un fonction simple qui permettrait de retrouver une disposition à partir de son numéro.
Je m'explique.
Il y a par exemple 10 façons de positionner 2 bleus parmi 5 :
:triste: :triste: :hein: :hein: :hein:
:triste: :hein: :triste: :hein: :hein:
:triste: :hein: :hein: :triste: :hein:
:triste: :hein: :hein: :hein: :triste:
:hein: :triste: :triste: :hein: :hein:
etc ...
On affecte à chaque "façon" un numéro de 1 à 10. Peut on facilement retrouver la position des 2 bleus à partir de ce simple numéro ? Soit ici une fonction de [1,10] vers [1,5]x[1,5]
Je cherche bien sur une formule dans le cas général p,n.
Merci de votre collaboration.
Bonjour. Le problème estr très intéressant.
Je commence par étudier le cas n=5. Déjà, je pense qu'il est naturel de numéroter ainsi (je ne dis pas que cette numérotation est la plus simple pour résoudre le problème) :
p=1 :triste: :triste: :id: :id: :id: ( -> (1,2) )
p=2 :triste: :id: :triste: :id: :id: ( -> (1,3) )
p=3 :triste: :id: :id: :triste: :id: ( -> (1,4) )
p=4 :triste: :id: :id: :id: :triste: ( -> (1,5) )
p=5 :id: :triste: :triste: :id: :id: ( -> (2,3) )
.
.
.
Ensuite, je pense à trois choses : à du modulo, à de l'écriture dans une base, et à de la récursivité. On peut remarquer que par exemple, si on prend comme convention que le premier élément du couple que la fonction renvoie est le pion bleu le plus à gauche, alors il y a 4 cas : selon que p soit entre 1 et 4 (large), entre 5 et 7, entre 8 et 9 ou que p=10. On remarque qu'à chaque fois l'intervalle diminue d'une unité (je ne sais pas si tout cela estr très clair, mais cela se voit très facilement si on dessine toutes les combinaisons).
Je n'ai pas grand chose de plus pour le moment, je vais continuer de chercher en tout cas, le problème est intéressant.
Je commence par étudier le cas n=5. Déjà, je pense qu'il est naturel de numéroter ainsi (je ne dis pas que cette numérotation est la plus simple pour résoudre le problème) :
p=1 :triste: :triste: :id: :id: :id: ( -> (1,2) )
p=2 :triste: :id: :triste: :id: :id: ( -> (1,3) )
p=3 :triste: :id: :id: :triste: :id: ( -> (1,4) )
p=4 :triste: :id: :id: :id: :triste: ( -> (1,5) )
p=5 :id: :triste: :triste: :id: :id: ( -> (2,3) )
.
.
.
Ensuite, je pense à trois choses : à du modulo, à de l'écriture dans une base, et à de la récursivité. On peut remarquer que par exemple, si on prend comme convention que le premier élément du couple que la fonction renvoie est le pion bleu le plus à gauche, alors il y a 4 cas : selon que p soit entre 1 et 4 (large), entre 5 et 7, entre 8 et 9 ou que p=10. On remarque qu'à chaque fois l'intervalle diminue d'une unité (je ne sais pas si tout cela estr très clair, mais cela se voit très facilement si on dessine toutes les combinaisons).
Je n'ai pas grand chose de plus pour le moment, je vais continuer de chercher en tout cas, le problème est intéressant.
Mais attend, en fait c'est trop bête ! Pourquoi ne pas associer à chaque combinaison son écriture en base 2 !
Par exemple
:id: :id: :triste: :id: :triste: correspondrait à 00101, et donc à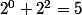 (j'ai pris le bit de poids faible à droite).
(j'ai pris le bit de poids faible à droite).
Et donc après, tu décomposes simplement 5 en base 2, et tu retrouves les positions ! Non ?
Evidemment, tu n'importe quelle base convient.
Par exemple
:id: :id: :triste: :id: :triste: correspondrait à 00101, et donc à
Et donc après, tu décomposes simplement 5 en base 2, et tu retrouves les positions ! Non ?
Evidemment, tu n'importe quelle base convient.
Maks a écrit:Mais attend, en fait c'est trop bête ! Pourquoi ne pas associer à chaque combinaison son écriture en base 2 !
Par exemple
:id: :id: :triste: :id: :triste: correspondrait à 00101, et donc à(j'ai pris le bit de poids faible à droite).
Et donc après, tu décomposes simplement 5 en base 2, et tu retrouves les positions ! Non ?
Evidemment, tu n'importe quelle base convient.
Merci d'avoir regardé.
Mon problème n'est pas d'associer à une configuration un chiffre qui me permet de retrouver cette configuration, car la bien sur,on peut coder à l'aide d'une base quelconque comme tu l'as dit.
Ce que je cherche c'est, sachant qu'il y a 10 configurations, comment retrouver simplement la 8e, ou la 4e ?
Mais regarde, il y a déjà un problème dans ce que tu racontes ! Tu parles de 4ième et de 8ième configuration ... mais quelle est-ta relation d'ordre ?! Pour pouvoir parler de 1er, 2ième, ... 3ième, il faut introduire une relation d'ordre, ce que tu n'as pas fait, et ce qui n'a rien d'évident pour des combinaisons.
Et bien tu utilises ma méthode :
Tu associes à chaque combinaison son codage en base b, puis sa valeur. Tu obtiens alors un codage du type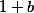 (11000),
(11000), 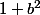 (10100), ..., puis tu ramènes ces valeurs sur l'intervalle 1..10. Je ne vois pas pourquoi cela ne convient pas ...
(10100), ..., puis tu ramènes ces valeurs sur l'intervalle 1..10. Je ne vois pas pourquoi cela ne convient pas ...
PS : j'ai maintenant pris le bit de poids faible à gauche, pour garder ton ordre.
Tu associes à chaque combinaison son codage en base b, puis sa valeur. Tu obtiens alors un codage du type
PS : j'ai maintenant pris le bit de poids faible à gauche, pour garder ton ordre.
Pas forcement une fonction mathématique explicite, plutot une technique pour retrouver la position mais qui marche dans le cas général, on te dit tu as 3 pions bleus et 9 places, il y a donc 84 positions différentes où sont les pions bleus dans la 55e position ?
La méthode pour retrouver les emplacements des pions bleus doit etre la meme quels que soient le nombre de pions bleus et le nombre de places.
Je ne sais pas si je suis clair ...
La méthode pour retrouver les emplacements des pions bleus doit etre la meme quels que soient le nombre de pions bleus et le nombre de places.
Je ne sais pas si je suis clair ...
Salut
--------------------------------------
compteur=0
rang=3 (pour trouver la 3eme posibilité)
boucle valeur_a_tester de 0 à 31 // (5 chiffres en binaire)
{
if ( nombre_de_un_en_binaire(valeur_a_tester) == 2 ) then compteur=compteur+1
if ( rang = compteur ) then afficher valeur_a_tester ; break
}
--------------------------------------
Çà marche bien quand n est petit mais quand n est grand les calculs risquent d'être un peu longs.
On obtient l'ordre suivant :
1) 00011
2) 00101
3) 00110
4) 01001
5) 01010
6) 01100
7) 10001
8) 10010
9) 10100
10) 11000
--------------------------------------
compteur=0
rang=3 (pour trouver la 3eme posibilité)
boucle valeur_a_tester de 0 à 31 // (5 chiffres en binaire)
{
if ( nombre_de_un_en_binaire(valeur_a_tester) == 2 ) then compteur=compteur+1
if ( rang = compteur ) then afficher valeur_a_tester ; break
}
--------------------------------------
Çà marche bien quand n est petit mais quand n est grand les calculs risquent d'être un peu longs.
On obtient l'ordre suivant :
1) 00011
2) 00101
3) 00110
4) 01001
5) 01010
6) 01100
7) 10001
8) 10010
9) 10100
10) 11000
adrd a écrit:Salut
--------------------------------------
compteur=0
rang=3 (pour trouver la 3eme posibilité)
boucle valeur_a_tester de 0 à 31 // (5 chiffres en binaire)
{
if ( nombre_de_un_en_binaire(valeur_a_tester) == 2 ) then compteur=compteur+1
if ( rang = compteur ) then afficher valeur_a_tester ; break
}
--------------------------------------
Çà marche bien quand n est petit mais quand n est grand les calculs risquent d'être un peu longs.
On obtient l'ordre suivant :
1) 00011
2) 00101
3) 00110
4) 01001
5) 01010
6) 01100
7) 10001
8) 10010
9) 10100
10) 11000
Oui, c'est la solution que je vais sans doute finir par adopter, qui revient à coder la position en base 2, puis à ne sélectionner que les nombres ayant le "bon nombre de 1", mais ça fait comme tu dis une boucle sur 2^n éléments, qui peut devenir très importante par rapport au nombre de positions, C(n,p).
On peut aussi procéder avec une fonction récursive, comme l'avait suggéré Maks, mais je n'ai rien trouvé de plus simple.
Une métode simple pour obtenir une valeur approchée.
Donner aux combis une valeur binaire, et classer selon ces valeurs binaires.
Appliquer cette formule pour retrouver le rang Rk d'une combinaison donnée Ck
Rk= MIN + (MAX-MIN)/C(n,p)*Ck
MAX= valeur binaire la plus élevée
MIN= valeur binaire la plus faible
Ck est la valeur binaire de la combi donnée.
Cette formule ne donne qu'une valeur approchée, et pas forcément exacte, les écarts entre les valeurs binaires des combis successives n'étant pas réguliers.
Sinon, pour trouver la valeur réelle, ça me parait difficile de trouver une formule correcte.
Donner aux combis une valeur binaire, et classer selon ces valeurs binaires.
Appliquer cette formule pour retrouver le rang Rk d'une combinaison donnée Ck
Rk= MIN + (MAX-MIN)/C(n,p)*Ck
MAX= valeur binaire la plus élevée
MIN= valeur binaire la plus faible
Ck est la valeur binaire de la combi donnée.
Cette formule ne donne qu'une valeur approchée, et pas forcément exacte, les écarts entre les valeurs binaires des combis successives n'étant pas réguliers.
Sinon, pour trouver la valeur réelle, ça me parait difficile de trouver une formule correcte.
nodjim a écrit:Une métode simple pour obtenir une valeur approchée.
Donner aux combis une valeur binaire, et classer selon ces valeurs binaires.
Appliquer cette formule pour retrouver le rang Rk d'une combinaison donnée Ck
Rk= MIN + (MAX-MIN)/C(n,p)*Ck
MAX= valeur binaire la plus élevée
MIN= valeur binaire la plus faible
Ck est la valeur binaire de la combi donnée.
Cette formule ne donne qu'une valeur approchée, et pas forcément exacte, les écarts entre les valeurs binaires des combis successives n'étant pas réguliers.
Oui, surtout que ce qui m'intéressait était de partir de Rk pour retrouver Ck, et si on inverse ta formule, on n'est pas du tout sur de trouver un Ck qui soit une combi valide ...
Galax a écrit:Oui, surtout que ce qui m'intéressait était de partir de Rk pour retrouver Ck, et si on inverse ta formule, on n'est pas du tout sur de trouver un Ck qui soit une combi valide ...
ça marche aussi bien dans un sens ou dans l'autre, vu que c'est la formule d'une droite. Mais attention, ça restera une valeur approchée.
Trouver Ck sous forme décimale à partir de Rk est simple, transformer cette valeur décimale en binaire, très simple aussi. Trouver la valeur la plus proche d'une combi valide est simple, mais rien ne dit, hélas, que ce sera vraiment la bonne.
Une autre classification plus efficace, qui permet, par encadrements successifs, de retrouver une combi dans une liste.
Identification et classement des combinaisons.
Soit n éléments choisis dans un ensemble de p éléments. La formulation C(n,p) définit le nombre de combinaisons possibles.
C(n,p)=p!/(n!*(p-n)!).
Le problème est de classer ces différentes combinaisons de telle sorte qu'on puisse facilement retrouver une combinaison donnée à partir
du rang dans le classement défini, ou à l'inverse retrouver le rang à partir de la combinaison.
1) Représentation d'une combinaison
En binaire, les n éléments sont représentés par un 1 les autres par un 0. Donc, c'est un mot binaire à p bits et n "1".
Sens de lecture de gauche à droite, premier bit à gauche, p ième à droite.
2)Classement
En 2 temps:
a) selon la longueur L du mot. On définit la longueur L du mot comme le nombre de bits contenus entre les "1" extrêmes.
La longueur L varie donc de n à p. On classe de la plus petite longueur à la plus grande.
b) selon la position P du 1er "1". P varie de 1 (le premier 1 en position 1) à p-L+1.
Pour un mot de longueur L, il y a p-L+1 positions.
Pour un L et P donné, il y a un certain nombre de mots.
On fige les "1" extrêmes et on classe ceux qui sont à l'intérieur de la même façon que précédemment.
Avec bien sûr n-2 "1" dans L-2 bits.
3)Identification du rang.
L'intérêt de ce classement est qu'il est facile de trouver le nombre de mots pour un LP donné.
C'est C(n-2,L-2). Et pour un L donné: (p-L+1)*C(n-2,L-2)
En faisant la sommation pour L=n avec L=n+1, L=n+2,....on trouvera rapidement la longueur d'un mot d'un rang donné, par un encadrement large.
Ensuite, la recherche de P est aussi très rapide. L'encadrement sera alors plus fin.
Ensuite, on recommence l'opération de recherche du L à l'intérieur du LP trouvé.
Etc.
Identification et classement des combinaisons.
Soit n éléments choisis dans un ensemble de p éléments. La formulation C(n,p) définit le nombre de combinaisons possibles.
C(n,p)=p!/(n!*(p-n)!).
Le problème est de classer ces différentes combinaisons de telle sorte qu'on puisse facilement retrouver une combinaison donnée à partir
du rang dans le classement défini, ou à l'inverse retrouver le rang à partir de la combinaison.
1) Représentation d'une combinaison
En binaire, les n éléments sont représentés par un 1 les autres par un 0. Donc, c'est un mot binaire à p bits et n "1".
Sens de lecture de gauche à droite, premier bit à gauche, p ième à droite.
2)Classement
En 2 temps:
a) selon la longueur L du mot. On définit la longueur L du mot comme le nombre de bits contenus entre les "1" extrêmes.
La longueur L varie donc de n à p. On classe de la plus petite longueur à la plus grande.
b) selon la position P du 1er "1". P varie de 1 (le premier 1 en position 1) à p-L+1.
Pour un mot de longueur L, il y a p-L+1 positions.
Pour un L et P donné, il y a un certain nombre de mots.
On fige les "1" extrêmes et on classe ceux qui sont à l'intérieur de la même façon que précédemment.
Avec bien sûr n-2 "1" dans L-2 bits.
3)Identification du rang.
L'intérêt de ce classement est qu'il est facile de trouver le nombre de mots pour un LP donné.
C'est C(n-2,L-2). Et pour un L donné: (p-L+1)*C(n-2,L-2)
En faisant la sommation pour L=n avec L=n+1, L=n+2,....on trouvera rapidement la longueur d'un mot d'un rang donné, par un encadrement large.
Ensuite, la recherche de P est aussi très rapide. L'encadrement sera alors plus fin.
Ensuite, on recommence l'opération de recherche du L à l'intérieur du LP trouvé.
Etc.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
