Autour de la semblance

[Idriss]

Salut,

Soit .

La fonction qui a une matrice de associe son polynôme caractéristique, ne vérifient pas si alors et semblable.

Mais qu'en est-il de qui a une matrice de associe le couple rang et polynôme caractéristique ?

Je me permets de motiver l'énigme, si la réponse est positive alors on aurait un moyen facile de savoir si 2 graphes sont isomorphes, problème réputer difficile de crypto.

[L.A.]

Bonsoir,

en regardant du côté des formes de Jordan (qui sont de vrais invariants de similitudes), je pense que non :

et

ont même rang 4 et même polynôme caractéristique (X-1)^4, mais ne sont pas semblables.

[GaBuZoMeu]

La réponse est négative.
Les matrices et ont même rang et même polynôme caractéristique mais ne sont pas semblables.
Deux matrices carrées de même taille sont semblables si et seulement si elles ont mêmes invariants de similitude. Dans le cas de la première des matrices ci-dessus, la liste des invariants de similitudes est . Dans le cas de la deuxième, c'est .

Le début de la réponse est le même que la réponse de L.A. .
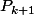
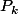
Les invariants de similitude sont une liste de polynômes unitaires où divise . Le premuier est le polynôme minimal, et leur produit est le polynôme caractéristique.

[Idriss]

Bravo à vous 2.

Deux matrices carrées de même taille sont semblables si et seulement si elles ont mêmes invariants de similitude.

Ce résultat est-il récent ?


Alors le problème d'isomorphisme des graphes est casser.

[GaBuZoMeu]

Absolument pas récent, c'est un grand classique, et ça ne "casse" pas le problème d'isomorphisme des graphes.

[Idriss]

Et pourtant en travaillant dans le corps à 2 éléments ?

A moins que la similitude ne fasse pas forcément dans le corps de départ, mais dans une extension de ce corps.

[GaBuZoMeu]

Le calcul des invariants de similitude d'une matrice se fait sur le corps de base, pas de souci de ce côté. C'est le calcul de la forme normale de Smith de la matrice . La complexité polynomiale de ce calcul me semble acquise (à vérifier).
Mais ce qui me cause souci, c'est que tu sembles penser que deux graphes dont les matrices d'adjacence sont semblables sont isomorphes. As-tu une démonstration, ou une référence de démonstration, de ceci ?

[Idriss]

Mais ce qui me cause souci, c'est que tu sembles penser que deux graphes dont les matrices d'adjacence sont semblables sont isomorphes. As-tu une démonstration, ou une référence de démonstration, de ceci ?

Oui, 2 matrices d’adjacence de même rang sont semblables (dans le corps à 2 éléments), ce qui ne donne pas un pouvoir de discernement énorme.

[GaBuZoMeu]

Oui, 2 matrices d’adjacence de même rang sont semblables (dans le corps à 2 éléments), ce qui ne donne pas un pouvoir de discernement énorme.

Je ne vois pas immédiatement pourquoi.
En tout cas, tu es bien d'accord que ton espoir de "casser" le problème d'isomorphisme de graphes tombe à l'eau ?

[Idriss]

1/ Je ne vois pas immédiatement pourquoi.

2/ En tout cas, tu es bien d'accord que ton espoir de "casser" le problème d'isomorphisme de graphes tombe à l'eau ?

1/ les matrices d'adjacences sont symétriques, donc diagonalisables.

2/ Pour cette voie oui, mais on peut construire tout un tas d'indicateur qui permette de savoir si on n'a pas isomorphisme, et donc par la même avoir une certaine certitude sur le fait que les graphes sont isomorphes ou non, mais bon la question ne m'intéresse pas plus que cela.

[GaBuZoMeu]

1/ les matrices d'adjacences sont symétriques, donc diagonalisables.

Oh la ! Erreur ! Ce sont les matrices RÉELLES symétriques qui sont diagonalisables, pas les matrices symétriques à coefficients dans . Saurais-tu diagonaliser sur ?

[Idriss]

Saurais-tu diagonaliser sur ?

Oui, si ta matrice était diagonalisable elle serait l'identité, car la seule valeur propre possible est 1 (non nul), en effet ta matrice est inversible (pas de valeur propre nul).

[GaBuZoMeu]

OK, donc tu es bien d'accord que ton argument n'est pas valable ? Voici d'ailleurs un contre-exemple :
Les deux matrices d'adjacence et ont même rang et ne sont pas semblables sur .

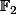
[Idriss]

Mais et sont déjà des contre-exemples

[GaBuZoMeu]

Non, puisque la deuxième n'est pas une matrice d'adjacence.

[Idriss]

Sommet ={1,2} et Arrête={(1,1),(2,2)}

[GaBuZoMeu]

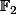
Manque de pot, la matrice d'adjacence dans ce cas est (chaque sommet est de valence 2). Tu ne peux considérer une matrice d'adjacence à coefficients dans que dans le cas d'un graphe simple (pas de boucle, pas d'arête multiple).

[Idriss]

Oui, c'est une question de choix de définition, et je n'adopte pas la même que la tienne, c'est tout.

Pour moi dans ce cas on a la matrice identité.

[GaBuZoMeu]

Arêtes et pas arrêtes.
Par contre, tu devrais arrêter parce que tu commences à raconter n'importe quoi. La matrice d'adjacence de ton dernier exemple est . Tu trouves vraiment qu'elle est de même rang que ?

PS. Ce qui est au-dessus, c'est une réponse à une bêtise que tu avais écrite et que tu t'es dépêché d'effacer.
Je réponds maintenant à ce que tu as écrit à la place : oui, c'est une question de définition. Celle que j'utilise est celle qu'utilisent les mathématiciens travaillant en théorie des graphes.

[Idriss]

J'ai édité mon message.

Oui, c'est une question de choix de définition, et je n'adopte pas la même que la tienne, c'est tout.

Pour moi dans ce cas on a la matrice identité.