Analyse
16 messages
- Page 1 sur 1
Analyse
Bonjour
Je propose ce petit exercice d'analyse (niveau L1-math sup)
Soit f : [0,1]→[0,1] une fonction t.q | f (x)− f (y)| ≤ |x−y| for all
x, y ∈ [0,1].
Montrer que l'ensemble des points fixes est soit un singleton ou bien intervalle.
Je propose ce petit exercice d'analyse (niveau L1-math sup)
Soit f : [0,1]→[0,1] une fonction t.q | f (x)− f (y)| ≤ |x−y| for all
x, y ∈ [0,1].
Montrer que l'ensemble des points fixes est soit un singleton ou bien intervalle.
Re: Analyse
j'essaie
supposons que a et b soient deux points fixes
Montrons que si a<x<b alors x est un point fixe
|f(x)-f(a)|<=|x-a| donne |f(x)-a|<=x-a
donc f(x)<=a+x-a
f(x)<=x
de même
|f(x)-b|<=b-x
f(x)>=b-(b-x)
f(x)>=x
Finalement f(x)=x
Ca me paraît un peu trop simple ....
supposons que a et b soient deux points fixes
Montrons que si a<x<b alors x est un point fixe
|f(x)-f(a)|<=|x-a| donne |f(x)-a|<=x-a
donc f(x)<=a+x-a
f(x)<=x
de même
|f(x)-b|<=b-x
f(x)>=b-(b-x)
f(x)>=x
Finalement f(x)=x
Ca me paraît un peu trop simple ....
Re: Analyse
Ok @chan, c'est quasiment ça mais il manque quelques éléments pour bien finir l'exo.
De plus dans le cas de l'intervalle que peut-on dire de plus?
De plus dans le cas de l'intervalle que peut-on dire de plus?
Re: Analyse
On montre facilement que f est continue sur [0;1] dans [0;1]. Elle admet donc au moins un point fixe.
On considère la borne inférieure m et la borne supérieure n de l'ensemble des points fixes.
Si m et n sont différents, on montre que tout élément de ]m;n[ est un point fixe (voir mon message précédent) puis que l'ensemble des points fixes est [m;n] en utilisant la continuité de f en m et n.
Donc soit il y a un seul point fixe, soit l'ensemble des points fixes et un intervalle fermé.
Exemples ci-dessous avec le graphe de f en bleu et les points fixes en rouge.
Cas d'un singleton:
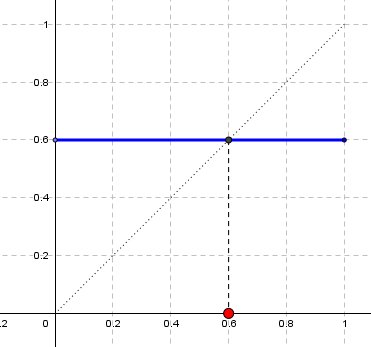
Cas d'un intervalle fermé:
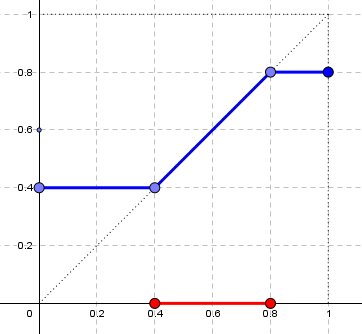
On considère la borne inférieure m et la borne supérieure n de l'ensemble des points fixes.
Si m et n sont différents, on montre que tout élément de ]m;n[ est un point fixe (voir mon message précédent) puis que l'ensemble des points fixes est [m;n] en utilisant la continuité de f en m et n.
Donc soit il y a un seul point fixe, soit l'ensemble des points fixes et un intervalle fermé.
Exemples ci-dessous avec le graphe de f en bleu et les points fixes en rouge.
Cas d'un singleton:

Cas d'un intervalle fermé:

Re: Analyse
il me semble qu'on peut généraliser :
avec continuité
-> soit un point, soit un intervalle unique fermé (le premier cas étant inclus dans le second)
sans hypothèse de continuité, pas de point fixe obligatoire mais on a
-> soit aucun point fixe, soit un point isolé, soit un intervalle unique qui peut être non fermé(même remarque).
avec continuité
-> soit un point, soit un intervalle unique fermé (le premier cas étant inclus dans le second)
sans hypothèse de continuité, pas de point fixe obligatoire mais on a
-> soit aucun point fixe, soit un point isolé, soit un intervalle unique qui peut être non fermé(même remarque).
Re: Analyse
Salut
Il me semble qu'avec la condition de l'énoncé, f est nécessairement continue sur [0,1]
Si on fixe y
soit strictement positif quelconque, si on prend |x-y|<
strictement positif quelconque, si on prend |x-y|< alors |f(x)-f(y)|<=|x-y|<
alors |f(x)-f(y)|<=|x-y|<
f est donc continue en y.
Il me semble qu'avec la condition de l'énoncé, f est nécessairement continue sur [0,1]
Si on fixe y
soit
f est donc continue en y.
Re: Analyse
@chan D'accord pour ta solution
Je ne suis pas du tout d'accord avec ça. On perd une hypothèse important par rapport à l'exercice.
Ce n'est pas très difficile d'exhiber un contrexemple.
pascal16 a écrit:il me semble qu'on peut généraliser :
avec continuité
-> soit un point, soit un intervalle unique fermé (le premier cas étant inclus dans le second)
Je ne suis pas du tout d'accord avec ça. On perd une hypothèse important par rapport à l'exercice.
Ce n'est pas très difficile d'exhiber un contrexemple.
Re: Analyse
Rebonjour
L'hypothèse dit que f est 1-lipschitzienne et cela implique la continuité. La réciproque est fausse.
L'hypothèse dit que f est 1-lipschitzienne et cela implique la continuité. La réciproque est fausse.
Re: Analyse
Salut,
S'il y en a qui veulent chercher un truc semblable, dans un vieux post. on s'était posé la question suivante :
Soient f et g deux fonctions continues de [0,1] dans [0,1] telles que fog=gof.
Existe-t-il forcément (au moins) un x de [0,1] tel que f(x)=x=g(x) ?
Sachant que la question au départ était uniquement de montrer qu'il y avait au moins un x de [0,1] tel que f(x)=g(x)
Je n'ai ni preuve, ni contre exemple . . .
S'il y en a qui veulent chercher un truc semblable, dans un vieux post. on s'était posé la question suivante :
Soient f et g deux fonctions continues de [0,1] dans [0,1] telles que fog=gof.
Existe-t-il forcément (au moins) un x de [0,1] tel que f(x)=x=g(x) ?
Sachant que la question au départ était uniquement de montrer qu'il y avait au moins un x de [0,1] tel que f(x)=g(x)
Je n'ai ni preuve, ni contre exemple . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Analyse
Bonjour, j'ai regardé et c'est pas évident du tout.
Ce qui est assez flippant dans cette question c'est le côté abstrait de l'hypothèse fog=gof.
Ce qui est assez flippant dans cette question c'est le côté abstrait de l'hypothèse fog=gof.
Re: Analyse
Ben314 a écrit:Salut,
S'il y en a qui veulent chercher un truc semblable, dans un vieux post. on s'était posé la question suivante :
Soient f et g deux fonctions continues de [0,1] dans [0,1] telles que fog=gof.
Existe-t-il forcément (au moins) un x de [0,1] tel que f(x)=x=g(x) ?
Sachant que la question au départ était uniquement de montrer qu'il y avait au moins un x de [0,1] tel que f(x)=g(x)
Je n'ai ni preuve, ni contre exemple . . .
Salut
Pas facile déjà de trouver des exemples
Avec f(x)=1/4 et g(x)=x , un seul point fixe commun: 1/4
Avec f(x)=x² et g(x)=
Avec f(x)=-4x²+4x et g(x)=3/4, un point fixe commun: 3/4
Il y a une démonstration connue avec par exemple l'hypothèse supplémentaire: f décroissante.
On pose h(x)=f(x)-x
h est strictement décroissante sur [0;1]
h(0)=f(0)>=0
h(1)=f(1)-1<=0
il existe un unique a dans [0;1] tel que h(a)=0 et on a f(a)=a
g(f(a))=g(a)
g(f(a)=f(g(a))
donc f(g(a))=g(a) et h(g(a))=0 et donc enfin g(a)=a
finalement f(a)=g(a)=a
Autre démonstration (pas de moi) dans le cas où f est croissante:
g, continue de [0,1] dans [0;1] admet un point fixe b.
soit la suite:
x(0)=b
x(1)=f(x(0))
x(n+1)=f(x(n))
Comme f est croissante, la suite x(n) est croissante si x(0)<=x(1) ou décroissante dans le cas contraire. Comme elle est bornée, elle converge vers un nombre a et comme f est continue, on a f(a)=a.
g(x(0))=g(b)=b
g(x(1))=g(f(x(0))=f(g(x(0)))=f(b)=x(1)
on procède par récurrence
si g(x(n)))=x(n)
g(x(n+1))=g(f(x(n)))=f(g(x(n)))=f(x(n)))=x(n+1)
donc g(x(n))=x(n) pour tout n
Comme x(n) converge vers a et comme g est continue, g(a)=a
donc f(a)=g(a)=a
Re: Analyse
De souvenirs de nos anciennes discussions sur le sujet, il en était sorti un lien vers un article construisant un contrexemple... Mais effectivement, construire des fonctions qui commutent c'est forcément un peu ch*** et à l'époque je n'avais pas eu la motivation de me plonger dans l'article en question. Mais donc en tout cas, si vous voulez continuer à réfléchir sur la question je vous conseille de chercher à prouver que la réponse est non 
Re: Analyse
Bon, ben me voila rassuré : j'étais persuadé que c'était vrai et j'avais bien l'air con à pas arriver à le prouver . . .
Après, si le contre exemple est pourri, je sais pas si je vais trop chercher . . .
Après, si le contre exemple est pourri, je sais pas si je vais trop chercher . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
