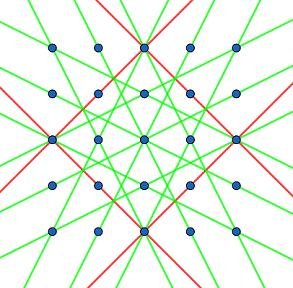
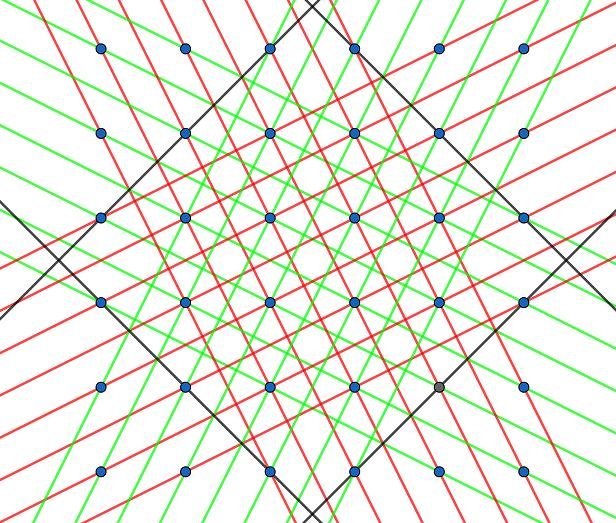
Je vais quand même essayer d’expliquer pourquoi
= \frac{1}{2} (f(m,n,j+1)-2f(m,n,j)+f(m,n,j-1)))
pour
))
Avec
=\sum_{pgcd(x,y)=1 \atop -n< kx<n ; -m< ky<m} (n-|kx|)(m-|ky|))
Cela revient exactement à l’idée de Doraki.
Soit

et

tel que
=1)
On va s’intéresser uniquement aux droites parallèles de la grille où les points successifs sont séparés par un décalage de

sur l’axe des abscisses et

sur l’axe des ordonnées. On dira que la distance entre deux points sur une droite de ce type est

si le décalage entre eux est de
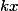
sur l’axe des abscisses et
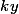
sur l’axe des ordonnées.
Pour une ligne qui contient

points, on note
)
le nombre de couple de points à distance

et
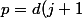-2d(j)+d(j-1))
-si
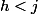
alors la distance max est
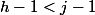
donc
=d(j)=d(j+1)=0)
et
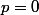
-si
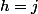
alors la distance max est
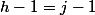
donc
=1)
;
=d(j+1)=0)
et
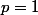
-si
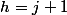
alors la distance max est
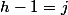
donc
=2)
car on peut prendre le premier et l’avant dernier ou le deuxième et le dernier ;
=1)
;
=0)
et
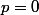
-si
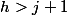
alors la distance max est
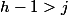
donc
=h-(j-1))
car on peut prendre tous les points sauf les
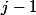
derniers qui n’auront plus de successeurs à la bonne distance ;
=h-j)
;
=h-(j+1))
et
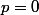
Au final

ne vaut 1 que lorsque
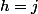
donc uniquement lorsqu’il y a

points sur la ligne et c’est ce qui nous intéresse !
Dans la grille, le nombre total de couple de points à distance

est
=(n-|kx|)(m-|ky|))
si
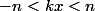
et
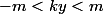
;
=0)
sinon. On peut en déduire que le nombre de droites passant par exactement

points et vérifiant le décalage
)
vaut
-2g(j)+g(j+1))
.
Finalement on s'intéresse aux autres droites en sommant tous les décalages possibles pour retrouver la formule voulue. Comme pour chaque couple
)
on aura le couple
)
il faut diviser par 2.
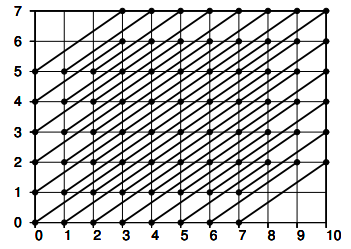
Exemple avec
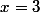
et
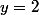
On trouve bien
=(11-3)(8-2)=48)
couples de points avec aucun point entre eux
=(11-2\times 3)(8-2\times 2)=20)
couples de points séparés par un point
=(11-3\times 3)(8-3\times2)=4)
couples de points séparés par 2 points
Le nombre de droites passant par exactement
2 points est
-2g(2)+g(1)=4-2\times 20 + 48 = 12)
3 points est
-2g(3)+g(2)=0-2\times 4 +20 = 12)
4 points est
-2g(4)+g(3)=0-2\times 0+4=4)
Voilà, j’espère que c’était à peu prés clair, j’ai essayé de faire au mieux