Question ~énigme

[zuko]

slt!
un sous groupe du réseau LinkedIn "the math connection", dt je suis membre pose des questions théoriques intéressantes. Je suis tombé sur cette question:
http://www.linkedin.com/groups/What-is-true-difference-between-1872005.S.275373759?qid=3688131a-1710-4108-989c-ef55f9e586d7&trk=groups_guest_most_popular-0-b-ttl&goback=%2Egmp_1872005

quelle est la "vraie" différence entre 1 et 0.999... ?

la grande majorité des membres a répondu d'une certaine manière alors que je suis partisan de l'autre réponse, je me demande si des mathématiciens plus jeunes répondent comme eux. que trouvez vous? sachant que "vraie" tel que indiqué ds la question introduit une marge d'interprétation mais je pense qu'il faut entendre "vraie" au sens mathématique.

[Ben314]

Pour moi, la différence entre 1 et 0,999... est exactement la même qu'entre par exemple 1/2 et 2/4 : c'est exactement la même chose écrite de deux manières différentes avec à la rigueur une des deux écriture qui est plus "standard" que l'autre : 1 est plus "standard" que 0,999... et 1/2 est plus "standard" que 2/4.

Par contre, un truc que je comprendrais jamais, c'est pourquoi il y a autant de personnes pour qui trouvent "bizare" d'écrire que 0.999...=1 alors que les mêmes personnes trouvent ça parfaitement "normal" d'écrire 1/2=2/4 ou bien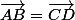 voire même pour .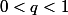
Donc je répondrais à la question par... une autre question : Pourquoi la non unicité de l'écriture en base 10 d'un réel pose elle autant de problème alors que la non unicité de l'écriture d'un quotient ou la non unicité des représentants d'un vecteur ne semble poser de problème à personne ?

[zuko]

soir'
pour commencer mon intéret est de comprendre pas forcément de convaincre, d'ailleurs j'aurais du mal à démontrer.
La question est posée par un docteur en maths pour le plaisir de discuter maths je pense. Pour répondre à géotype, je pense que la question est posée de manière à appeler éventuellement diverses réponses selon qu'on se place dans tel ou tel ensemble.

personnellement je le concois ainsi : 0,999... a un infinité de décimales mais est différent de 1 car
1-0,999... = 0,000... [qqchose] # 0
il reste une différence infinitésimale car même si 0,999... continue jusqu'à l'infini il n'atteint jamais 1.
Donc la différence est un "epsilon" infiniment petit.

@Ben314, je pense que 1/2=2/4 sans aucun doute mais par contre si on écrit 1/3=0.333... théoriquement et strictement cela est faux. Car 1/3 est le nombre "complet" alors qu'il manque tjrs un epsilon infiniment petit à 0.333... Je pense que 1/3=0.333... devrait être concu comme un appercu du nombre donné par une calculette par exemple.
qu'en pensez vous? :zen:
sur LinkedIn la majorité a répondu comme BEN et géotype, mais une grande minorité a conclu comme moi, avec des démonstations plus rigoureuses et compliquées cela dit

[Monsieur23]

Aloha,

personnellement je le concois ainsi : 0,999... a un infinité de décimales mais est différent de 1 car
1-0,999... = 0,000... [qqchose] # 0
il reste une différence infinitésimale car même si 0,999... continue jusqu'à l'infini il n'atteint jamais 1.
Donc la différence est un "epsilon" infiniment petit.

0,999… est égal à 1, et 1 - 0,99… = 0.

Je dirais donc comme Ben, ce sont juste deux écritures différentes du même réel.

[beagle]

"il reste une différence infinitésimale car même si 0,999... continue jusqu'à l'infini il n'atteint jamais 1. "

il y a ici un problème d'espace temps,
car 0,999... ne tend pas vers 1, il n'est pas dans le temps, pour aller quelque part il faut commencer à partir et arriver plus tard ailleurs,
sauf que le 0,999... ne se déplace pas vers 1, il est déjà là, est-ce que le 2 bouge?Mais où va le 2 ce matin?jamais entendu parlé de ça moi.
donc 0,999... ne va nulle part , il est là au bout de ma distance unitaire de 1, ou bien il est un quelque chose d'entier, un stylo, un ...
ce qui est choquant, c'est que c'est l'humain qui regarde le 0,999... immobile lui, et qui pour l'inspecter, le voir, le décrire, va se balader de 9 en 9,
mais c'est l'humain qui tend vers 1 dans ce voyage, le 0,999 ne bouge pas il est déjà là tout entier 1.

[Ben314]

personnellement je le concois ainsi : 0,999... a un infinité de décimales mais est différent de 1 car
1-0,999... = 0,000... [qqchose] # 0
il reste une différence infinitésimale car même si 0,999... continue jusqu'à l'infini il n'atteint jamais 1.
Donc la différence est un "epsilon" infiniment petit.

Le fond du problème réside dans les mots soulignés çi dessus : comme pas mal de personnes depuis une petite cinquantaine d'année (précisément depuis que les traveaux de georg cantor ont été à peu prés acceptés par la comunauté mathématique), tu parle "d'infini" et "d'infinité" comme s'il sagisait d'une notion "naturelle" et naïve (comme la notion d'entier naturel par exemple).
Sauf que, si on reste sur un point de vue "naïf" des math, c'est à dire si on considère par exemple que les entiers naturels, c'est ce qui permet de compter des "vrais" objets, alors il est évident que l'infini n'existe pas (au sens naïf).
Si on "force" son existence au sens naïf, donc sans axiomes, on tombe trés rapidement sur pas mal de contradictions.

Tout ça pour dire que, si on revenait une petite centaine d'année en arrière, personne ne se poserait la question de savoir si, "naïvement parlant", on a 0.999...=1 ou pas pour une raison extrèmement simple : il n'y a pas moyen de définir "naïvement" ce que veut dire "0.999... avec une infinité de 9"
Donc la seule et unique façon de voir la question est de considérer un cadre axiomatique, c'est à dire de commencer par donner une définition carée-carée de ce que l'on entend par 0.9999....
Et là, il n'y a pas tellement le choix : 0.9999... (avec une infinité de 9) ne peut clairement se définir que comme la limite lorsque n tend vers l'infini de Un=0.999...9 (avec n fois le chiffre 9). Et le mot "limite" est quand à lui défini par "pour tout epsilon>0, il existe N tel que...". Avec cette définition là de 0.999... on démontre extrèmement façilement que 0.999...=1.

Si tu préfère, vu dans l'autre sens, je ne peut absolument pas démentir ta phrase " 0,999... a un infinité de décimales mais est différent de 1" vu que... tu ne donne aucune définition de l'objet 0.999... et, évidement, temps que l'on ne donne pas de définition claire de ce que représente un objet x (par exemple 0.999...), ben on ne risque pas de montrer que cet objet là vaut (ou ne vaut pas) une quantité donnée.
Donc, ta phrase "0.9999... est différent de 1" a exactement le même statut que la phrase "le réel X est différent de 1", c'est à dire quen, sans précision sur qui est X, on ne risque pas de montrer que cette phrase est vrai... ni qu'elle est fausse.
Conclusion : Quelle est pour toi la définition de 0.999... (avec une infinité de 9) ?

[beagle]

Il faut certainement faire ce que dit Ben314, rigueur de définition, rigueur de démonstration.

Si on a une bonne culture maths cela doit suffire pour convaincre.

Maintenant si on se place à un niveau inférieur, on ne peut pas s'en sortir intuitivement tant que l'on reste sur une opération non finie, tant que l'on reste sur du tend vers.
On ne peut se persuader que cela fait vraiment 1 qu'une fois l'addition répétée à l'infinie enin achevée.
c'est ce que je voulais dire par en mouvement ou pas.
regarder les 9 qui défilent, les accompagner mentalement, c'est se condamner à examiner une somme infinie à un moment où l'opération n'est pas finie.alors oui, à ce moment là, il y a bien un petit chouille qui n'est pas le 1.
donc terminez l'opération infinie, placez-vous à la fin,
et à la fin est le 1

Oui, mais je ne peux pas me placer à la fin de l'infini.
ben si.
si on reprend le fil de discussion sur le paradoxe de zénon, 1/2 puis 1/2 de 1/2, puis encore 1/2 du reste and so on,
cette addition infinie si on la regarde en train de s'effectuer, on a le sentiment d'aller au 1, mais on a aussi le sentiment qu'il manquera toujours un chouille pour ètre 1.
et pourtant lorsque l'addition est terminée, cela fait bien 1.
et lorsque je me déplace d'un point A au point B, je fais bien la moitié du chemin, puis la moitié du reste puis la moitié du reste, je fais cela à l'infini, et cela ne me rapproche pas de plus en plus de B, j'arrive une fois ceci terminé à B (et au-delà si pas fatigué!).

si je fais cela en coloriant une surface d'unité 1.
Surface est blanche, je vais colorier en noir la moitié puis la moitié puis la moitié restante.
Lorsque l'infini aura tout colorié, A LA FIN, tout est noir.s'il reste du blanc, je note sur la copie, travail insuffisant, à finir.j'ai dit la FIN.
ben à la fin, enfin, c'est 1

mème surface blanche,
je colorie 9/10 puis 9/100 puis 9 /1000, et je me place à la fin du coloriage,
c'est tout noir aussi, à la fin est le 1.

bref, c'est bien d'utiliser les limites, le truc qui tend vers,
mais les gens faut les prendre par la main et les mettre devant le travail fini.
si on leur montre le boulot en construction, beaucoup n'arrivent pas à ètre convaincus.