Cherche mathématicien...
48 messages
- Page 2 sur 3 - 1, 2, 3
Re: Cherche mathématicien...
L'illustration est dispo à :
https://www.dropbox.com/s/d44tk6g4evk3t ... e.pdf?dl=0
https://www.dropbox.com/s/d44tk6g4evk3t ... e.pdf?dl=0
Re: Cherche mathématicien...
Salut,
En fait, je réalise que c'est un problème assez simple de droites, de perpendiculaires d'intersections de droites et de distances entre points que je devrais pouvoir arriver à résoudre moi-même, peut-être pas de façons très élégante, mais simplement fonctionnelle...
En fait, je réalise que c'est un problème assez simple de droites, de perpendiculaires d'intersections de droites et de distances entre points que je devrais pouvoir arriver à résoudre moi-même, peut-être pas de façons très élégante, mais simplement fonctionnelle...
Re: Cherche mathématicien...
Salut, Ben 314,
Je suis en train de traiter les cas particuliers et il y en a deux que j'ai du mal à résoudre.
Dans ton calcul des tangentes :
def Eq_Tangente_Parabole(P): # P=[a,b,c,d,e]=Parabole:(ax+by)^2+dx+ey+f avec a^2+b^2=1
d=P[0]*P[3]-P[1]*P[2]
return [(P[3]**2/4-P[1]**2*P[4])/d,(2*P[0]*P[1]*P[4]-P[2]*P[3]/2)/d,(P[2]**2/4-P[0]**2*P[4])/d,-P[1],P[0]]
# [a,b,c,d,e] où D:ux+vy+w=0 est une tangente à P ssi au^2+buv+cv^2+duw+evw=0
lorsque les deux paraboles ont leurs directrices parallèles à l'axe des X, d est alors égal à 0 et je ne sais alors pas trop quoi faire, ces équations étant hélas un peu absconses pour moi...
Autre problème, que je n'ai pas encore investigué, lorsque les directrices des deux paraboles sont strictement parallèles, distinctes ou non, aucune tangente n'est trouvée alors qu'il devrait en exister au moins une : je ne sais pas encore vraiment pourquoi.
Pour le reste, je crois avoir à peu près tout traité (je me suis focalisé surtout sur tout ce qui peut générer une division par zéro) : les foyers ne doivent pas être sur leurs directrices et les deux paraboles doivent êtres distinctes (dans ce cas précis, d'ailleurs, on a aussi d=0) .
En dehors de ces deux soucis, tout fonctionne à merveille semble-t-il et je n'ai plus qu'à implémenter la validation finale, à savoir si la tangente générée est "pliable" ou non, comme j'ai tenté de te l'expliquer dans mes deux précédents messages.
Des idées ?
Cordialement,
F.
Je suis en train de traiter les cas particuliers et il y en a deux que j'ai du mal à résoudre.
Dans ton calcul des tangentes :
def Eq_Tangente_Parabole(P): # P=[a,b,c,d,e]=Parabole:(ax+by)^2+dx+ey+f avec a^2+b^2=1
d=P[0]*P[3]-P[1]*P[2]
return [(P[3]**2/4-P[1]**2*P[4])/d,(2*P[0]*P[1]*P[4]-P[2]*P[3]/2)/d,(P[2]**2/4-P[0]**2*P[4])/d,-P[1],P[0]]
# [a,b,c,d,e] où D:ux+vy+w=0 est une tangente à P ssi au^2+buv+cv^2+duw+evw=0
lorsque les deux paraboles ont leurs directrices parallèles à l'axe des X, d est alors égal à 0 et je ne sais alors pas trop quoi faire, ces équations étant hélas un peu absconses pour moi...
Autre problème, que je n'ai pas encore investigué, lorsque les directrices des deux paraboles sont strictement parallèles, distinctes ou non, aucune tangente n'est trouvée alors qu'il devrait en exister au moins une : je ne sais pas encore vraiment pourquoi.
Pour le reste, je crois avoir à peu près tout traité (je me suis focalisé surtout sur tout ce qui peut générer une division par zéro) : les foyers ne doivent pas être sur leurs directrices et les deux paraboles doivent êtres distinctes (dans ce cas précis, d'ailleurs, on a aussi d=0) .
En dehors de ces deux soucis, tout fonctionne à merveille semble-t-il et je n'ai plus qu'à implémenter la validation finale, à savoir si la tangente générée est "pliable" ou non, comme j'ai tenté de te l'expliquer dans mes deux précédents messages.
Des idées ?
Cordialement,
F.
Re: Cherche mathématicien...
Je regarde petit à petit.
1) Concernant l'équation permettant de savoir si une droite donnée est ou pas une tangentes à une parabole donnée, il n'y a aucun cas particulier : ça marche "à tout les coups", que d soit nul ou pas ne change rien.
Et si ça déconne concernant le cas des directrices parallèles, ça provient de ce que je t'avais écrit dans le post du 21 octobre à 16h03 : tu as à résoudre l'équation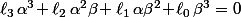 et il y a un cas particulier numérique à traiter si
et il y a un cas particulier numérique à traiter si 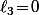 .
.
Dans le truc python, vu le solveur rustique que j'ai tapé qui ne marche que et exclusivement que pour les équation de degré 3, cette équation est envoyé au "solveur" sous la forme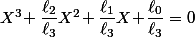 qui bien évidement ne marche que si
qui bien évidement ne marche que si 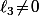 et ça ne trouve pas les solutions avec
et ça ne trouve pas les solutions avec 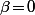 .
.
1) Concernant l'équation permettant de savoir si une droite donnée est ou pas une tangentes à une parabole donnée, il n'y a aucun cas particulier : ça marche "à tout les coups", que d soit nul ou pas ne change rien.
Et si ça déconne concernant le cas des directrices parallèles, ça provient de ce que je t'avais écrit dans le post du 21 octobre à 16h03 : tu as à résoudre l'équation
Dans le truc python, vu le solveur rustique que j'ai tapé qui ne marche que et exclusivement que pour les équation de degré 3, cette équation est envoyé au "solveur" sous la forme
Modifié en dernier par Ben314 le 17 Nov 2018, 17:16, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
1/ Sauf que si d=0, la division est illégale et c'est le cas si les deux directrices sont // à l'axe des x 
2/ Compris : si l3=0, j'ai alors à résoudre une simple équation du 2d degré (donc 1 ou 2 racines). C'est bien ça ?

2/ Compris : si l3=0, j'ai alors à résoudre une simple équation du 2d degré (donc 1 ou 2 racines). C'est bien ça ?
Re: Cherche mathématicien...
Je ne comprend pas de quelfdesar a écrit:1/ Sauf que si d=0, la division est illégale et c'est le cas si les deux directrices sont // à l'axe des x
Dans ton précédent message vu que tu cité la procédure "Eq_Tangente_Parabole", j'avais l'impression que tu parlait du
Sauf que ça a rien a voir avec ce dont tu parle maintenant correspondant aux cas de DEUX paraboles...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
C'est dans le calcul des tangentes communes que ça se produit :
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])/d
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2])/d; c=(T1[2]*T2[4]-T1[4]*T2[2])/d
S=Solve([a,b,c]); R=[]
for s in S:
d=sqrt(s**2+1); a=s/d; b=1/d;
R.append([a,b,-(T1[0]*a**2+T1[1]*a*b+T1[2]*b**2)/(T1[3]*a+T1[4]*b)]);
return R
Si les deux directrices sont // à l'axe des ordonnées, alors d=0 car j'ai :
T1[0]=-172.44965
T2[3]=0.00000
T1[3]=0.00000
T2[0]=-212.48255
(soit le 'c' de chaque tangente égal à zéro) d'où le d=0.
Mais j'ai aussi d=0 si les deux paraboles sont confondues avec :
T1[0]=41.44129
T2[3]=0.15546
T1[3]=0.15546
T2[0]=41.44129
ou là, T1[0]*T2[3] = T1[3]*T2[0]
Je pensais détecter ce cas de cette façon, et c'est là que j'ai découvert le problème précédent.
...
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])/d
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2])/d; c=(T1[2]*T2[4]-T1[4]*T2[2])/d
S=Solve([a,b,c]); R=[]
for s in S:
d=sqrt(s**2+1); a=s/d; b=1/d;
R.append([a,b,-(T1[0]*a**2+T1[1]*a*b+T1[2]*b**2)/(T1[3]*a+T1[4]*b)]);
return R
Si les deux directrices sont // à l'axe des ordonnées, alors d=0 car j'ai :
T1[0]=-172.44965
T2[3]=0.00000
T1[3]=0.00000
T2[0]=-212.48255
(soit le 'c' de chaque tangente égal à zéro) d'où le d=0.
Mais j'ai aussi d=0 si les deux paraboles sont confondues avec :
T1[0]=41.44129
T2[3]=0.15546
T1[3]=0.15546
T2[0]=41.44129
ou là, T1[0]*T2[3] = T1[3]*T2[0]
Je pensais détecter ce cas de cette façon, et c'est là que j'ai découvert le problème précédent.
...
Re: Cherche mathématicien...
Bis et répéta....
Ces formules là en rouge :
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])/d
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2])/d; c=(T1[2]*T2[4]-T1[4]*T2[2])/d
C'est celle du post du 21 Oct 2018 16:03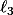 (c'est à dire le d de la procédure Tangente_Commune) est nul, ben on avait plus affaire à une équation de degré 3 en
(c'est à dire le d de la procédure Tangente_Commune) est nul, ben on avait plus affaire à une équation de degré 3 en 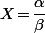 mais à une solution particulière
mais à une solution particulière 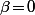 plus une équation du second degré en
plus une équation du second degré en 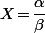 .
.
Et j'avais bien précisé dans le post du 27 Oct 2018 22:53 où j'avais mis le truc en python que ce cas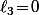 n'était pas traité par le programme pour pas passer 3 plombes à taper tout les les cas particuliers.
n'était pas traité par le programme pour pas passer 3 plombes à taper tout les les cas particuliers.
Ces formules là en rouge :
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])/d
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2])/d; c=(T1[2]*T2[4]-T1[4]*T2[2])/d
C'est celle du post du 21 Oct 2018 16:03
où j'avais parfaitement précisé que, siBen314 a écrit:Ensuite, on calcule :
=> une droiteest tangente commune ssi
ce qui donne la fameuse éqaution du troisième degré à résoudre en
et avec la solution particulière
si
Et j'avais bien précisé dans le post du 27 Oct 2018 22:53 où j'avais mis le truc en python que ce cas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
Bref, pour tenir compte des cas particuliers, il faut mettre :
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1]
b=T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2]; c=T1[2]*T2[4]-T1[4]*T2[2]
Si d est non nul résoudre l'équation de degré 3 : X^3+a/d.X^2+b/d.X+c/d =0 pour trouver les pentes alpha/beta solutions du problème.
Si d est nul alors ajouter la solution "beta=0" et résoudre l'équation de degré 2 : X^2+b/a.X+c/a = 0 pour trouver les autres pentes alpha/beta solutions du problème.
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
d=T1[0]*T2[3]-T1[3]*T2[0]; a=T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1]
b=T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2]; c=T1[2]*T2[4]-T1[4]*T2[2]
Si d est non nul résoudre l'équation de degré 3 : X^3+a/d.X^2+b/d.X+c/d =0 pour trouver les pentes alpha/beta solutions du problème.
Si d est nul alors ajouter la solution "beta=0" et résoudre l'équation de degré 2 : X^2+b/a.X+c/a = 0 pour trouver les autres pentes alpha/beta solutions du problème.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
Merci, et vraiment désolé pour mon incompréhension, ça dépasse très largement mon niveau :
je n'avait absolument pas compris que d était le calcul de l3, a celui de l2, b de l1 et c de l0

Juste une petite précision (je suis vraiment TRÈS nul), tu écris "Si d est nul alors ajouter la solution "beta=0" et résoudre l'équation de degré 2 : X^2+b/a.X+c/a = 0 pour trouver les autres pentes alpha/beta solutions du problème." : cela signifie-t-il que si l3=0 alors il s'agit de trouver la solution beta=0 en résolvant l'équation ou y a-t-il encore un cas particulier à traiter pour beta=0 ?
Je suis un peu dur de la comprenette, mais je t'avais prévenu... en tous cas, merci pour ta patience.
je n'avait absolument pas compris que d était le calcul de l3, a celui de l2, b de l1 et c de l0


Juste une petite précision (je suis vraiment TRÈS nul), tu écris "Si d est nul alors ajouter la solution "beta=0" et résoudre l'équation de degré 2 : X^2+b/a.X+c/a = 0 pour trouver les autres pentes alpha/beta solutions du problème." : cela signifie-t-il que si l3=0 alors il s'agit de trouver la solution beta=0 en résolvant l'équation ou y a-t-il encore un cas particulier à traiter pour beta=0 ?
Je suis un peu dur de la comprenette, mais je t'avais prévenu... en tous cas, merci pour ta patience.
Re: Cherche mathématicien...
Re-salut,
J'ai bien résolu le cas où l3=0 en résolvant l'équation du 2d degré que tu m'as indiquée, mais je tombe finalement sur un dernier cas particulier : celui où en plus, l0=0.
j'en conclue que la tangente doit exister, être unique et être un horizontale, donc que a = 0 et b = 1
mais je n'arrive pas à trouver la valeur de c...
C'est très probablement trivial, mais j'aurais encore besoin d'un petit coup de main...
Merci d'avance,
F.
J'ai bien résolu le cas où l3=0 en résolvant l'équation du 2d degré que tu m'as indiquée, mais je tombe finalement sur un dernier cas particulier : celui où en plus, l0=0.
j'en conclue que la tangente doit exister, être unique et être un horizontale, donc que a = 0 et b = 1
mais je n'arrive pas à trouver la valeur de c...
C'est très probablement trivial, mais j'aurais encore besoin d'un petit coup de main...
Merci d'avance,
F.
Re: Cherche mathématicien...
.
Modifié en dernier par Ben314 le 19 Nov 2018, 21:19, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
Merci beaucoup : ça semble marcher dans tous les cas maintenant. Au final, ça donne quelque chose comme ça :
Ça te paraît correct ou bien aurais-je laissé passer quelque chose ?
Je te dois une fière chandelle et au passage j'ai appris plein de choses !
- Code: Tout sélectionner
def Tangente_Commune(T1,T2): #T1,T2=[a,b,c,d,e]=Eqaution au^2+buv+cv^2+duw+evw=0
R=[]
d=T1[0]*T2[3]-T1[3]*T2[0];
if d != 0 # 0-3 tangentes communes, cas général
a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])/d
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2])/d;
c=(T1[2]*T2[4]-T1[4]*T2[2])/d
S=Solve3([a,b,c]);
for s in S:
d=sqrt(s**2+1);
a=s/d;
b=1/d;
R.append([a,b,-(T1[0]*a**2+T1[1]*a*b+T1[2]*b**2)/(T1[3]*a+T1[4]*b)]);
return R
else
a=(T1[0]*T2[4]-T1[4]*T2[0]+T1[1]*T2[3]-T1[3]*T2[1])
if a != 0 # 0-2 tangentes communes, dont les tangentes verticales pour lesquelles s=0
b=(T1[1]*T2[4]-T1[4]*T2[1]+T1[2]*T2[3]-T1[3]*T2[2]);
c=(T1[2]*T2[4]-T1[4]*T2[2])
S=Solve2([b/a,c/a]);
for s in S:
R.append([s,1,-(T1[0]*a**2+T1[1]*a*b+T1[2]*b**2)/(T1[3]*a+T1[4]*b)]);
return R
else # 1 tangente commune horizontale
R.append([0,1,-(T1[0]*a**2+T1[1]*a*b+T1[2]*b**2)/(T1[3]*a+T1[4]*b)]);
Ça te paraît correct ou bien aurais-je laissé passer quelque chose ?
Je te dois une fière chandelle et au passage j'ai appris plein de choses !
Re: Cherche mathématicien...
J'ai encore trouvé un cas particulier (que j'espère être le dernier !) :
celui ou l3, l1 et l0 sont tous trois égaux à 0.
C'est le cas où les deux foyers sont sur la même verticale et les deux directrices sont aussi sur une même verticale (distincte de la première, bien sûr).
La solution pour la tangente unique est alors a=1, b=0 et pour c, je ne peux pas utiliser l'équation de T1 car T1[3] est aussi égal à 0, ce qui me donne T1[3]*$a+$t1[4]*$b=0. J'utilise alors l'équation de T2 pour trouver la valeur de c car T2[3] != 0...
Ça te paraît-il cohérent ou bien devrais-je aussi tester lequel de T1[3] ou T2[3] est != 0 ? Y aurait-il un cas possible où les deux seraient égaux à zéro ?
Dommage que ton message du 19 Nov 2018 à 18:41 ait été effacé, il m'avait aidé à comprendre pas mal de choses...
Merci d'avance pour tes conseil, en espérant ne pas trop raconter d'absurdités.
F.
celui ou l3, l1 et l0 sont tous trois égaux à 0.
C'est le cas où les deux foyers sont sur la même verticale et les deux directrices sont aussi sur une même verticale (distincte de la première, bien sûr).
La solution pour la tangente unique est alors a=1, b=0 et pour c, je ne peux pas utiliser l'équation de T1 car T1[3] est aussi égal à 0, ce qui me donne T1[3]*$a+$t1[4]*$b=0. J'utilise alors l'équation de T2 pour trouver la valeur de c car T2[3] != 0...
Ça te paraît-il cohérent ou bien devrais-je aussi tester lequel de T1[3] ou T2[3] est != 0 ? Y aurait-il un cas possible où les deux seraient égaux à zéro ?
Dommage que ton message du 19 Nov 2018 à 18:41 ait été effacé, il m'avait aidé à comprendre pas mal de choses...
Merci d'avance pour tes conseil, en espérant ne pas trop raconter d'absurdités.
F.
Re: Cherche mathématicien...
Le message du 19 c'est moi qui l'ai effacé en faisant ce que je fais (hélas...) souvent : j'ai voulu le "citer" pour récupérer les formules qu'il y a dedans et en fait je l'ai "modifié" et perdu.
Le message du 19 c'est moi qui l'ai effacé en faisant ce que je fais (hélas...) souvent : j'ai voulu le "citer" pour récupérer les formules qu'il y a dedans et en fait je l'ai "modifié" et perdu.
Sinon, en regardant de plus prés l'équation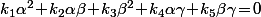 qui caractérise les tangentes
qui caractérise les tangentes 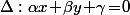 qui sont tangentes à la parabole donnée, si on l'écrit directement en partant de la directrice
qui sont tangentes à la parabole donnée, si on l'écrit directement en partant de la directrice 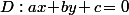 et des coordonnées
et des coordonnées ) du foyer, ça donne ça :
du foyer, ça donne ça :
\alpha^2\!+\!(ax_F\!-\!by_F\!+\!c)\beta^2\!-\!2(ay_F\!+\!bx_F)\alpha\beta\!-\!2(a\alpha\!+\!b\beta)\gamma\!=\!0)
Où on voit que, si on veut trouver partant de
partant de  et
et  , c'est à dire trouver l'unique tangente à la parabole qui a une de direction donnée, il faut que
, c'est à dire trouver l'unique tangente à la parabole qui a une de direction donnée, il faut que 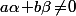 c'est à dire que la direction de
c'est à dire que la direction de  ne soit pas orthogonale à celle de
ne soit pas orthogonale à celle de  (ce qui est parfaitement normal vu qu'il n'y a aucune tangente perpendiculaire à la directrice).
(ce qui est parfaitement normal vu qu'il n'y a aucune tangente perpendiculaire à la directrice).
Donc dans ton calcul final pour retrouver en fonction de
en fonction de  et
et  , si ça conduit à une division par zéro, ça signifie qu'il n'y a pas de tangente commune ayant cette direction là. Et ce n'est pas la peine d'essayer la division avec l'autre formule vu que ça donne forcément aussi une division par 0 (en fait, on tombe sur ce cas particulier lorsque les deux directrices sont parallèles).
, si ça conduit à une division par zéro, ça signifie qu'il n'y a pas de tangente commune ayant cette direction là. Et ce n'est pas la peine d'essayer la division avec l'autre formule vu que ça donne forcément aussi une division par 0 (en fait, on tombe sur ce cas particulier lorsque les deux directrices sont parallèles).
A part ce cas particulier là, toutes les autres solutions de l'équation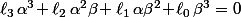 conduisent à de "vraies" solutions (c'est à dire à une tangente commune).
conduisent à de "vraies" solutions (c'est à dire à une tangente commune).
Si par exemple tu as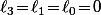 alors ton programme doit
alors ton programme doit
1) Repérer que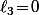 ce qui donne une première solution
ce qui donne une première solution 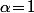 ;
; 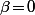 .
.
2) Résoudre l'équation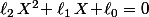 d'inconnue
d'inconnue 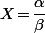 qui, vu le cas particulier présent est
qui, vu le cas particulier présent est 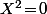 qui donne une unique solution
qui donne une unique solution 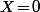 c'est à dire
c'est à dire 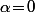 ;
; 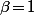 .
.
3) Pour chacun des deux couples trouvés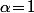 ;
; 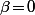 et
et 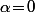 ;
; 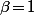 regarder si le calcul du
regarder si le calcul du  correspondant conduit ou pas à une division par 0. Si oui, la solution n'est pas bonne.
correspondant conduit ou pas à une division par 0. Si oui, la solution n'est pas bonne.
Et si effectivement tes directrices sont toute les deux verticales (donc parallèles), tu aura forcément une "fausse solution" avec une tangente commune perpendiculaire aux directrices, c'est à dire horizontale donc au niveau calculs, la solution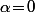 ;
; 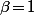 sera rejetés pour cause de "division par zéro".
sera rejetés pour cause de "division par zéro".
Le message du 19 c'est moi qui l'ai effacé en faisant ce que je fais (hélas...) souvent : j'ai voulu le "citer" pour récupérer les formules qu'il y a dedans et en fait je l'ai "modifié" et perdu.
Sinon, en regardant de plus prés l'équation
Où on voit que, si on veut trouver
Donc dans ton calcul final pour retrouver
A part ce cas particulier là, toutes les autres solutions de l'équation
Si par exemple tu as
1) Repérer que
2) Résoudre l'équation
3) Pour chacun des deux couples trouvés
Et si effectivement tes directrices sont toute les deux verticales (donc parallèles), tu aura forcément une "fausse solution" avec une tangente commune perpendiculaire aux directrices, c'est à dire horizontale donc au niveau calculs, la solution
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
ça semble à peu près coller avec ce que j’obtiens, à savoir que tout fonctionne sauf le cas tout à fait précis où les deux directrice sont // ET confondues ET verticales ET que les deux foyers sont tous deux situés sur une MÊME verticale (distincte de celle des directrices). Je dois alors forcer la valeur de a à 0, de b à 1 (puisque j’ai forcémment une tangente verticale) et calculer c avec l’équation pour laquelle je n’ai pas de division par 0...
Si dans cet énoncé précédent, je remplace « verticale » par « horizontale » le problème ne semble pas survenir : l3=0, mais l0 !=0. Je résous alors l’équation du 2nd degré et trouve alors deux tangentes, alors qu’il ne devrait y en avoir qu’une, il me semble...
Ce que je ne comprends pas, c’est pourquoi dans le cas « tout horizontal » j’ai deux tangentes que je trouve naturellement alors que dans le cas « tout vertical » je suis obligé de considérer qu’il n’en existe qu’une seule que je dois calculer « à l’arrache » en forçant a=0, b=1 !
Si dans cet énoncé précédent, je remplace « verticale » par « horizontale » le problème ne semble pas survenir : l3=0, mais l0 !=0. Je résous alors l’équation du 2nd degré et trouve alors deux tangentes, alors qu’il ne devrait y en avoir qu’une, il me semble...
Ce que je ne comprends pas, c’est pourquoi dans le cas « tout horizontal » j’ai deux tangentes que je trouve naturellement alors que dans le cas « tout vertical » je suis obligé de considérer qu’il n’en existe qu’une seule que je dois calculer « à l’arrache » en forçant a=0, b=1 !
Re: Cherche mathématicien...
Bonjour, Ben,
J'aurais besoin d'un dernier petit coup de main concernant les tangentes à une parabole.
Je cherche à résoudre un "problème" sur lequel je sèche depuis plusieurs heures (et c'est un euphémisme), alors que je sais que pour toi ce sera évident en quelques minutes.
J'ai donc une parabole P dont je connais les chi) calculés par la méthode que tu m'as indiquée précédemment.
calculés par la méthode que tu m'as indiquée précédemment.
Je connais un point p(x,y) et je cherche à trouver, si elles existent, la ou les droites tangentes à P (peu importe leurs directions) et passant par le point p. Je dois donc, en fait, résoudre -- si je ne me trompe pas -- le système d'équation à trois inconnues (il y a peut-être plus simple ?) :

avec (a, b, c) comme inconnues, et là, je sèche : je ne sais pas par quel bout le prendre.
Si tu pouvais avoir la grande bonté de me dire déjà si je ne me trompe pas dans mon raisonnement et surtout comment trouver la solution, je t'en serais grandement reconnaissant.
Cordialement
J'aurais besoin d'un dernier petit coup de main concernant les tangentes à une parabole.
Je cherche à résoudre un "problème" sur lequel je sèche depuis plusieurs heures (et c'est un euphémisme), alors que je sais que pour toi ce sera évident en quelques minutes.
J'ai donc une parabole P dont je connais les chi
Je connais un point p(x,y) et je cherche à trouver, si elles existent, la ou les droites tangentes à P (peu importe leurs directions) et passant par le point p. Je dois donc, en fait, résoudre -- si je ne me trompe pas -- le système d'équation à trois inconnues (il y a peut-être plus simple ?) :
avec (a, b, c) comme inconnues, et là, je sèche : je ne sais pas par quel bout le prendre.
Si tu pouvais avoir la grande bonté de me dire déjà si je ne me trompe pas dans mon raisonnement et surtout comment trouver la solution, je t'en serais grandement reconnaissant.
Cordialement
Re: Cherche mathématicien...
C'est un peu toujours la même chose : l'équationfdesar a écrit:
Bref, il faut regarder uniquement les deux autres et là, vu que la deuxième est linéaire, on peut l'utiliser facilement pour substituer une variable et le plus simple est évidement de l'écrire
La dernière donne alors
C'est à dire
Et on procède comme d'habitude c'est à dire en posant
Et en traitant à part le cas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cherche mathématicien...
Merci !
Le passage par a=tb ne m’était pas venu à l’esprit (je n’en avait aucun souvenir) ce qui fait que je me retrouvait avec 2 inconnues dont je n’arrivais pas à me dépétrer (d’où mon idée idiote d’introduire la première équation de normalisation qui ne faisait en fait que compliquer les choses).
En tous cas merci encore : j’apprends vraiment beaucoup et c’est très clair.
Le passage par a=tb ne m’était pas venu à l’esprit (je n’en avait aucun souvenir) ce qui fait que je me retrouvait avec 2 inconnues dont je n’arrivais pas à me dépétrer (d’où mon idée idiote d’introduire la première équation de normalisation qui ne faisait en fait que compliquer les choses).
En tous cas merci encore : j’apprends vraiment beaucoup et c’est très clair.
48 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
