Valeurs approchées
16 messages
- Page 1 sur 1
Valeurs approchées
Bonjour à tous!
J'ai un devoir de maths dans lequel on me demande de trouver la valeur approchée de e (la constante de Napier), avec une précision qui n'est pas une puissance de 10.
Je dispose d'un encadrement :
(1+1/n)^n<= e <= (1+1/n)^(n+1)
Et la question est :
"Comment peut-on obtenir une valeur approchée à 10^(-3)/3 ?" Il n'est pas précisé que l'encadrement est à utiliser, mais je pense que si.
Voilà, je peux vous assurer que je cherche depuis plusieurs jours, et j'ai écumé tous les sites internet traitant des valeurs approchées! Malheureusement, mes recherches sont restées infructueuses... Je ne comprends pas comment avoir la précision demandée...
Merci d'avance!!
J'ai un devoir de maths dans lequel on me demande de trouver la valeur approchée de e (la constante de Napier), avec une précision qui n'est pas une puissance de 10.
Je dispose d'un encadrement :
(1+1/n)^n<= e <= (1+1/n)^(n+1)
Et la question est :
"Comment peut-on obtenir une valeur approchée à 10^(-3)/3 ?" Il n'est pas précisé que l'encadrement est à utiliser, mais je pense que si.
Voilà, je peux vous assurer que je cherche depuis plusieurs jours, et j'ai écumé tous les sites internet traitant des valeurs approchées! Malheureusement, mes recherches sont restées infructueuses... Je ne comprends pas comment avoir la précision demandée...
Merci d'avance!!
Re: Valeurs approchées
Salut,
Lorsque tu sait par exemple qu'un certain réel x est compris entre 3.1 et 3.18, une façon à peine différente de dire exactement la même chose, c'est de dire que x a pour valeur approchée 3.14 à 0.04 prés.
Donc là, ton inégalité, elle te dit qu'une valeur approchée de e c'est .... à .... prés (qui dépendent de n) et tu as juste à chercher pour quel n on a une précision inférieure ou égale à celle qui est demandée.
Lorsque tu sait par exemple qu'un certain réel x est compris entre 3.1 et 3.18, une façon à peine différente de dire exactement la même chose, c'est de dire que x a pour valeur approchée 3.14 à 0.04 prés.
Donc là, ton inégalité, elle te dit qu'une valeur approchée de e c'est .... à .... prés (qui dépendent de n) et tu as juste à chercher pour quel n on a une précision inférieure ou égale à celle qui est demandée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Valeurs approchées
Ok d'accord merci beaucoup, donc je pose mon équation
((1+1/n)^(n+1)-(1+1/n)^n ) / 2= 1/3000
(1+1/n)^n x 1/n = 1/1500, c'est bien ça?
((1+1/n)^(n+1)-(1+1/n)^n ) / 2= 1/3000
(1+1/n)^n x 1/n = 1/1500, c'est bien ça?
Re: Valeurs approchées
Ben314 a écrit:. . . et tu as juste à chercher pour quel n on a une précision inférieure ou égale à celle qui est demandée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Valeurs approchées
Bonjour,
Méthode straightforward ...
On trace à la calculette graphique le graphe de f(x) = (1+1/x)^x - e + 10^-3/3
et on regarde sur le graphe la valeur de x pour avoir f(x) = 0
... on lit : x = 4076,5...
Il faut donc n = 4077
Cela ne sera peut-être pas apprécié par les matheux ... mais c'est terriblement rapide et efficace.

Méthode straightforward ...
On trace à la calculette graphique le graphe de f(x) = (1+1/x)^x - e + 10^-3/3
et on regarde sur le graphe la valeur de x pour avoir f(x) = 0
... on lit : x = 4076,5...
Il faut donc n = 4077
Cela ne sera peut-être pas apprécié par les matheux ... mais c'est terriblement rapide et efficace.
Re: Valeurs approchées
A mon sens, c'est surtout terriblement couillon : si tu as une calculette qui connait e (ce qui est nécessaire vu que la fonction que tu trace contient cette constante), ben tu as qu'à lui demander d'afficher la valeur de e pour avoir e avec bien plus que la précision demandée par l'exo.Black Jack a écrit:Cela ne sera peut-être pas apprécié par les matheux ... mais c'est terriblement rapide et efficace.
Bref, ce type d'exo n'a de sens que si on fait les calculs à la main ou, à la rigueur, comme si on avait à sa disposition uniquement une calculatrice "4 opérations".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Valeurs approchées
Si on supprimait les exercices couillons dans ce qui est proposé dans l'enseignement secondaire ... il n'en resterait pas beaucoup.

Re: Valeurs approchées
Rebonjour,
Si on ne veut pas utiliser "e" pour calculer n, on peut mettre le graphe de f(x) = (1+1/x)^x - (1+1/x)^(x+1) + 2*10^-3/3 sur la calculette graphique ... et y lire la valeur de x pour laquelle f(x) = 0
On lit : x = 4076,9...
et on a donc n = 4077

Si on ne veut pas utiliser "e" pour calculer n, on peut mettre le graphe de f(x) = (1+1/x)^x - (1+1/x)^(x+1) + 2*10^-3/3 sur la calculette graphique ... et y lire la valeur de x pour laquelle f(x) = 0
On lit : x = 4076,9...
et on a donc n = 4077
Re: Valeurs approchées
Citation : donc je pose mon équation ((1+1/n)^(n+1)-(1+1/n)^n ) / 2= 1/3000
Oui et non.
Ce qu'on cherche, ce n'est pas , c'est
, c'est  .
.  n'est qu'une étape pour trouver
n'est qu'une étape pour trouver 
Même pas. Je corrige : n'est qu'une étape pour trouver un encadrement de
n'est qu'une étape pour trouver un encadrement de  , avec une certaine précision.
, avec une certaine précision.
On cherche en fait , tel que : ((1+1/n)^(n+1)-(1+1/n)^n ) / 2 <= 1/3000
, tel que : ((1+1/n)^(n+1)-(1+1/n)^n ) / 2 <= 1/3000
Du coup, tu peux tâtonner.
Si on choisit n=1000, on trouve un encadrement, mais la largeur de l'intervalle est trop grande.
Si on choisit n=5000 , ou n=10000, bingo... l'intervalle obtenu a une largeur qui correspond aux contraintes.
Oui et non.
Ce qu'on cherche, ce n'est pas
Même pas. Je corrige :
On cherche en fait
Du coup, tu peux tâtonner.
Si on choisit n=1000, on trouve un encadrement, mais la largeur de l'intervalle est trop grande.
Si on choisit n=5000 , ou n=10000, bingo... l'intervalle obtenu a une largeur qui correspond aux contraintes.
Re: Valeurs approchées
Bof
En utilisant la manière que j'ai préconisée, on trouve en quelques secondes que n = 4077 est la plus petite valeur de n telle que (1 + 1/n)^n est égal à e à moins de 1/3000 près.
... et bien entendu tout n >= 4077 aussi.
Connaître le but de la question posée serait bien.
Si c'est trouver la valeur de n minimale telle que (1 + 1/n)^n donne une valeur de e à moins de 1/3000 près, on peut faire comme je l'ai préconisé ... ou perdre du temps en tâtonnant en calculant avec des n différents jusqu'à ce que l'encadrement soit respecté juste en dessous de 1/3000.
Si c'est trouver une valeur de n quelconque qui donne une valeur de e à moins de 1/3000 près...
alors, on calcule l'encadrement avec un n et (n+1) très grand et c'est fini... mais je suis très sceptique que le but ait été celui-là.

En utilisant la manière que j'ai préconisée, on trouve en quelques secondes que n = 4077 est la plus petite valeur de n telle que (1 + 1/n)^n est égal à e à moins de 1/3000 près.
... et bien entendu tout n >= 4077 aussi.
Connaître le but de la question posée serait bien.
Si c'est trouver la valeur de n minimale telle que (1 + 1/n)^n donne une valeur de e à moins de 1/3000 près, on peut faire comme je l'ai préconisé ... ou perdre du temps en tâtonnant en calculant avec des n différents jusqu'à ce que l'encadrement soit respecté juste en dessous de 1/3000.
Si c'est trouver une valeur de n quelconque qui donne une valeur de e à moins de 1/3000 près...
alors, on calcule l'encadrement avec un n et (n+1) très grand et c'est fini... mais je suis très sceptique que le but ait été celui-là.
Re: Valeurs approchées
A mon avis (donc ça vaut ce que ça vaut...), ce qui est attendu, c'est un truc de ce style :
En prenant comme approximation de le milieu de l'intervalle où on sait qu'il est situé on a une précision au moins égale à la moitié de la largeur de l'intervalle donc on veut que :
le milieu de l'intervalle où on sait qu'il est situé on a une précision au moins égale à la moitié de la largeur de l'intervalle donc on veut que :
^{n+1}-\big(1\!+\!\frac{1}{n}\big)^{n}\Big]\leq \dfrac{1}{3000}=:\varepsilon\ \ \text{c'est \`a dire}\ \ \ n\geq\dfrac{1}{2\varepsilon}\big(1\!+\!\frac{1}{n}\big)^{n}\ (*))
Or on sait que, pour tout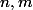 , on a
, on a ^{m+1}\geq e\geq \big(1\!+\!\frac{1}{n}\big)^{n}) donc, pour que (*) soit vérifiée, il suffit de prendre
donc, pour que (*) soit vérifiée, il suffit de prendre ^{m+1}) en prenant pour
en prenant pour  un entier quelconque, (par exemple
un entier quelconque, (par exemple 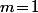 )
)
En prenant comme approximation de
Or on sait que, pour tout
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Valeurs approchées
Bonsoir à tous,
En tout cas, je vous remercie beaucoup pour vos conseils qui me sont très précieux. Je pense que je vais opter pour une approche du style :
- trouver n pour avoir la précision demandée
- supposer que e est situé au milieu de l'encadrement et donc faire la moyenne
- arrondir le résultat à la précision exigée.
Surtout qu'après j'ai un algorithme à rédiger pour généraliser tout ça. Je me demande aussi si je ne reprendrai pas la méthode graphique qui a été proposée, pour avoir une autre approche.
Bref, un grand merci!!
Bonne soirée à tous
En tout cas, je vous remercie beaucoup pour vos conseils qui me sont très précieux. Je pense que je vais opter pour une approche du style :
- trouver n pour avoir la précision demandée
- supposer que e est situé au milieu de l'encadrement et donc faire la moyenne
- arrondir le résultat à la précision exigée.
Surtout qu'après j'ai un algorithme à rédiger pour généraliser tout ça. Je me demande aussi si je ne reprendrai pas la méthode graphique qui a été proposée, pour avoir une autre approche.
Bref, un grand merci!!
Bonne soirée à tous
Re: Valeurs approchées
En revanche, je ne parviens pas à voir comment tu as pu obtenir une telle précision avec la lecture graphique, Black Jack... Ce n'est pas évident à lire.
Re: Valeurs approchées
Léa314159 a écrit:En revanche, je ne parviens pas à voir comment tu as pu obtenir une telle précision avec la lecture graphique, Black Jack... Ce n'est pas évident à lire.
Sur la plupart (toutes probablement) des calculettes graphiques, on peut définir la plage des abscisses visualisées.
On peut donc resserrer cette plage en 2 ou 3 fois vers l'endroit où on voit f(x) = 0 et ainsi affiner la lecture jusqu'à une précision suffisante.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
