2. Comment Résoudre un problème faisant intervenir les équations du premier degré à une inconnue.Certaines situations (ou énoncés) présentent un problème dans lequel nous disposons de plusieurs quantités qui interviennent ensemble. En général, ces quantités dépendent les unes des autres. Par exemple, nous avons que la somme de plusieurs prix fait tel, la somme de deux distances vaut telle valeur... Et puis on nous fournit un renseignement liant ces quantités entre elles.
La Résolution de tels énoncés se fait en 4 étapes.
1) Choix de l'inconnue: la quantité que l'on cherche. C'est vous qui choisissez le nom de cette inconnue ! x, y, z, j, v, t, k..?
Il est parfois plus simple de choisir comme inconnue la première lettre de l'objet dont on cherche de déterminer la valeur ; exemple: b pour billes, j pour joueurs, etc...
2) Mise en équation: Généralement l'étape la plus 'difficile'. Nous la verrons plus tard.
3) Résolution de l'équation: Résolution méthodique de l'équation en appliquant les règles de calcul...
4) Vérification: Vérification du résultat obtenu dans 2) et 3) en les confrontant aux hypothèses de l'énoncé
Voici deux exemples de problèmes difficiles et leur solution:
Problème1 a écrit:Dans une école il y a quatre classes de 4eme groupant en tout 112 eleves. Dans la classe de la 4eme B, il y a 5 élèves de plus qu'en 4eme A. Le rapport du nombre des élèves de 4eme C et celui de 4eme A est de 2/3, et la classe de 4eme D a 7 élèves de plus qu'en 4eme C. Calculer le nombre d'élèves dans chaque classe. (D'après "Mathématique quatrième année du cycle moyen" Prog Libanais, 1975)
Solution
Étape 1: Choix de l'inconnueSoit x le nombre d'élèves en 4e B. (On choisit une classe de référence. On aurait pu choisir la 4ème A, ou une autre section !)
Étape 2: Mise en ÉquationLe nombre d'élèves en 4e A est donc x - 5 (comme il y a 5 élèves en moins en 4e A qu'en 4e B).
Le rapport des élèves de 4e C et de 4eme A est de 2/3. Cela signifie que pour deux élèves en 4e C il y en a 3 en 4eme A. En calculant donc les 2/3 du nombre d'élèves en 4e A, on trouvera celui des élèves en 4e C. Or x - 5 est le nombre des élèves en 4eme A, donc celui des élèves en 4e C serait
)
soit donc
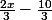
La 4e D possède 7 élèves de plus que la quatrième C. On peut donc dire qu'elle possède 2x/3 -10/3 + 7 élèves en tout.
Maintenant on sait que la somme des élèves de toutes les classes réunies est de 112.
L'équation à résoudre est donc la suivante:
(4ème A) + (4ème B) + (4ème C) + (4ème D) = 112
(x -5) + (x) + (2x/3 - 10/3) + (2x/3 - 10/3 + 7) = 112
Etape 3: Résolution de l'Équationx + (x - 5) + 2x/3 - 10/3 + 2x/3 - 10/3 + 7 = 112
2x - 5 + 2x/3 - 10/3 + 2x/3 - 10/3 + 7 = 112
2x + 4x/3 - 5 . - 20/3 + 7 = 112
10x/3- 20/3 + 2 = 112
10x/3- 20/3 = 110
10x- 20 = 330
10x = 350
x = 35.
Étape 4: Vérification et ConclusionLe nombre d'élèves en 4eme B semble être 35.
Celui en 4e A est donc 35 - 5 = 30.
Celui en 4e C correspond aux 2/3 de ce qu'il y a en 4ème A, donc 20 élèves.
Celui en 4e D est de 20 + 7 = 27.
La somme du nombre des élèves est de 35 + 30 + 20 + 27 = 112
Le problème a donc été bien résolu !
Problème2 a écrit:Déterminer deux entiers consécutifs sachant que la différence de leurs carres est de 225. (D'après "Mathématique quatrième année du cycle moyen" Prog Libanais, 1975)
Solution:
Étape 1: Choix de l'inconnueSoit x le premier nombre. Son successeur est donc x + 1.
Étape 2: Mise en équationLe carré du premier nombre est x². Le carré du second nombre est (x + 1)².
On a donc:
(x + 1)² - x² = 225 (On soustrait du plus grand, le plus petit)
Étape 3: Résolution de l'équationx² + 2x + 1 x² = 225
x² - x² + 2x + 1 = 225
2x = 224
x = 112
Étape 4: Conclusion et VérificationCes nombres semblent donc être 112 et 113.
112 et 113 sont deux entiers consécutifs. De plus, 113² - 112² = 225, doù 113 et 112 sont bien les nombres cherchés.
 ~
~  ~
~