pour l'équation (2):
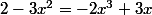
On écrit toutes les quantités à gauche du signe "égal":
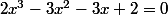
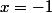
est
une solution évidente. Le polynôme
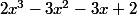
admet pour diviseur
))
soit
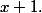
Faisons apparaitre
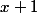
comme facteur commun:
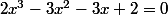
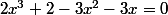
-3x(x+1)=0) (4)
(4)développons
(x^2-x+1)) (5)
(5)En remplaçant
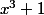
par le produit (5) dans l'équation (4) , on trouve
(x^2-x+1)-3x(x+1)=0)
on peut donc factoriser (x+1) dans l'équation.
Il vient l'équation produit nul:
(2x^2-5x+2)=0)
sais tu factoriser le trinôme
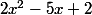
?
remarque: d'où vient le facteur
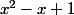
dans le produit
(5) ?

est la somme de trois termes d'une progression géométrique de raison -x et de premier terme 1:
on a donc
^3}{1-(-x)}=\dfrac{1+x^3}{1+x})
en multipliant les deux côtés par x+1, il vient:
(1-x+x^2)=1+x^3)
soit
(x^2-x+1)=x^3+1)

