Bonjour à toutes et tous
Je cherche en vain la reponse a ce probleme, assé difficile.
Merci infinniment de votre aide précieuse.
RECTANGLE ÉLASTIQUE
On a diminué la largeur et augmenté la longueur dun rectangle
dun même pourcentage entier.
Après cette déformation, laire du rectangle a diminué dun
pourcentage compris entre 2 % et 3 %.
De quel pourcentage a-t-on modifié la largeur et la longueur ?
Merci. Bonne apres midi et bonne continuation
JP.
Probleme 3e "rectangle élastique"
7 messages
- Page 1 sur 1
Jimmy Page a écrit:Bonjour à toutes et tous
Je cherche en vain la reponse a ce probleme, assé difficile.
Merci infinniment de votre aide précieuse.
RECTANGLE ÉLASTIQUE
On a diminué la largeur et augmenté la longueur dun rectangle
dun même pourcentage entier.
Après cette déformation, laire du rectangle a diminué dun
pourcentage compris entre 2 % et 3 %.
De quel pourcentage a-t-on modifié la largeur et la longueur ?
Merci. Bonne apres midi et bonne continuation
JP.
Tu as un rectangle de longueur L et de largeur l. Son aire est L * l
Puis l diminue de x% donc la nouvelle largeur l' = l * ...
Puis L augmente de x% donc la nouvelle longueur L' = L * ...
Et la nouvelle aire A' a diminué de y% donc A' = A * ...
Or A' = L' * l' et A = L * l => ça te donne une équation du 2° degré à une inconnue "x" et une valeur pas vraiment connue mais délimitée "y".
Calcul de delta, puis solutions x1 et x2 dont toutes deux dépendront de y => à mon avis, il faudra pas tâtonner longtemps sur les différentes valeurs possibles de y pour trouver x1 et x2 entiers !!!
Et en plus, étant donné que les valeurs sont interchangeables (on peut inverser l'augmentation de la longueur et la diminution de la largeur et obtenir la même surface) cela signifie que x1=-x2
Bonjour,
Soit la longueur ,
la longueur ,  la largeur et
la largeur et  l'aire du rectangle.
l'aire du rectangle.

Soit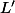 la nouvelle longueur. C'est L augmentée de
la nouvelle longueur. C'est L augmentée de 
où k est un entier.
)
il reste à calculer la nouvelle largeur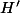 diminuée de
diminuée de  , et la nouvelle aire S' en fonction de S.
, et la nouvelle aire S' en fonction de S.
Tu devrais trouver que l'aire diminue de
grâce à l'identité remarquable:
(a-b)=a^2-b^2)
après on cherche les carrés entre 200 et 300 pour déterminer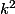 !
!
remarque: si tu écris la nouvelle aire S' fonction de S, tu t'aperçois d'un truc bizzarroïde:
si on augmente la largueur et on diminue la longueur d'un certain pourcentage,
l'aire diminue.
c'est logique.
mais si si on augmente la longueur et on diminue la largeur d'un certain pourcentage,l'aire diminue aussi. :zen:
exemple: prendre un rectangle de dimensions 6 et 12.
augmenter ou diminuer la longueur de 1/3.l'aire diminue dans les deux cas.
Soit
Soit
où k est un entier.
il reste à calculer la nouvelle largeur
Tu devrais trouver que l'aire diminue de
grâce à l'identité remarquable:
après on cherche les carrés entre 200 et 300 pour déterminer
remarque: si tu écris la nouvelle aire S' fonction de S, tu t'aperçois d'un truc bizzarroïde:
si on augmente la largueur et on diminue la longueur d'un certain pourcentage,
l'aire diminue.
c'est logique.
mais si si on augmente la longueur et on diminue la largeur d'un certain pourcentage,l'aire diminue aussi. :zen:
exemple: prendre un rectangle de dimensions 6 et 12.
augmenter ou diminuer la longueur de 1/3.l'aire diminue dans les deux cas.
mathelot a écrit:si on augmente la largueur et on diminue la longueur d'un certain pourcentage,
l'aire diminue.
T'es sûr ?
Prenons un rectangle L=10 et l=4 => S= 40
Augmentons la largeur de 2 et diminuons la longueur de 2 => L=8 et l=6 et S=48 :marteau:
mathelot a écrit:c'est logique.
Non, ça se calcule. En comparant L * l avec (L - x) * (l + x) ce qui donne x > L - l pour que ce soit vrai...
Sve@r a écrit:T'es sûr ?
Prenons un rectangle L=10 et l=4 => S= 40
Augmentons la largeur de 2 et diminuons la longueur de 2 => L=8 et l=6 et S=48 :marteau:
euh,non . Dans ton exemple, on augmente la largeur de 50%
et on diminue la longueur de 20%.
Jimmy Page a écrit:On a diminué la largeur et augmenté la longueur dun rectangle dun même pourcentage entier.
c'est le même différentiel, en pourcentage %.
l'aire diminue dans les deux cas.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
