Un problème qui paraissait facile

[apache1234]

Bonjour,

En lisant le problème de mon fils, le problème paraissait assez facile mais je ne suis pas du tout sur de moi, pouvez vous m'aider??!!

Voici le problème : Un triangle ABC a un périmètre de 18 cm, déterminer la distance du point I à la droite AI

Pas facile de détailler le problème sans afficher la figure.

Le triangle parait équilatéral puisque les 3 cotés sont identiques, il y a une droite qui continue la base du triangle (droite BC) de la même longueur qu'un coté du triangle pour former la droite CI (le point C est du coup le milieu de BI, et une droite relie le point I a A pour former la droite AI, et le triangle ACI

Pas très explicite ,Je peux vous donner un schéma par mail si vous avez besoin

Merci bcp.

[Lostounet]

Bonsoir!

Pourrais-tu héberger le schéma sur un site comme http://www.imageshack.us ?

[apache1234]

http://imageshack.us/photo/my-images/840/mathsug.jpg/

voici le lien si c'est comme ça

[Lostounet]

Tu cherches la distance du point I à la droite (AI) ? Et bien, elle est nulle car I est un point de cette droite.
C'est une faute de frappe je pense? :p

[apache1234]

heu oui je te tape l'énoncé a l'identique sachant que le périmètre du triangle ABC est égale a 18cm , déterminer a 0.01 cm près la distance du point I à la droite (AB) , justifier désolé :lol3:

[Frednight]

Il faut jouer sur les angles : les ronds, tracés par toi ou donnés directement, indiquent les côtés de longueur identique. Ainsi le triangle ABC est équilatéral et le triangle ACI est isocèle. Tu en déduis que et donc que . Et comme ACI est isocèle, tu as donc soit . L'angle 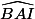est donc tel que .

Ton triangle BAI est donc rectangle, preuve à l'appui, et tu n'as qu'à appliquer pythagore.

[Lostounet]

Ou bien en exploitant le fait que dans un triangle rectangle, la médiane relative à l'hypoténuse a sa longueur qui en fait la moitié, on peut dire que ABI rectangle en A.
Par conséquent, la distance de I à (AB) est bien AI

Or d'après le th. de Pythagore, AI^2 + AB^2 = BI^2

On a AB et BI :)

[apache1234]

Merci les gars, j'avais la bonne démarche mais pas le vocabulaire pour expliquer de cette façons merci beaucoup